Как выделить целую часть числа
Дроби, у которых числитель меньше знаменателя, называются правильные дроби.
Дроби, у которых числитель больше либо равен знаменателю, называются неправильные дроби. Для неправильных дробей действует негласное правило, согласно которому необходимо в конце решения в обязательном порядке выделить целую часть. Для того чтобы выделить целую часть из неправильной дроби, нужно разделить числитель на знаменатель, записать целую часть перед дробью, посередине, остаток записать в числитель, а знаменатель оставить тем же.
Пример:  , где 1 -результат деления, а 2 -остаток от деления.
, где 1 -результат деления, а 2 -остаток от деления.
Некоторые действия с дробями требуют, наоборот, исключительно неправильных дробей. Среди них, в первую очередь – умножение и деление дробей. Для того чтобы превратить смешанную дробь (дробь, в которой присутствует целая часть) в неправильную дробь, необходимо целую часть умножить на знаменатель, прибавить к ней текущий числитель дроби – это и станет новым числителем. Знаменатель останется тем же.
Пример: 
В обоих случаях, если изначальная дробь была несократимой, то в результате у числителя и знаменателя также не найдется общих множителей.
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
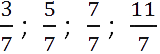 Обратите внимание, что в двух первых дробях (
Обратите внимание, что в двух первых дробях (
| 3 |
| 7 |
и
| 5 |
| 7 |
) числители меньше знаменателей. Такие дроби называют правильными.
У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробь
| 7 |
| 7 |
имеет числитель равный знаменателю (такие дроби равны единицы), а дробь
| 11 |
| 7 |
имеет числитель больший знаменателя. Такие дроби называют неправильными.
У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
Пример. Выделим целую часть из неправильной дроби
| 11 |
| 2 |
.
- Разделим в столбик числитель на знаменатель.
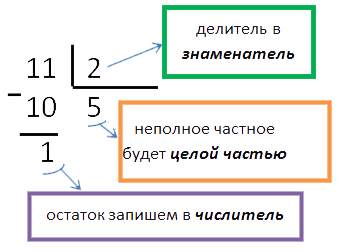
- Теперь запишем ответ.
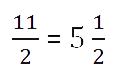
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
-
Умножаем целую часть на знаменатель.
3 · 5 = 15
Прибавляем числитель.
15 + 2 = 17
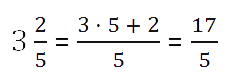
Любое смешанное число можно представить как сумму целой и дробной части.
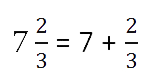
Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Разделы: Математика
Класс: 4
Основные цели:
- Сформировать способность к выделению целой части из неправильной дроби.
- Повторить понятия числителя и знаменателя, дроби правильные и неправильные, смешанные числа.
- Актуализировать умение выделять целую часть из неправильной дроби.
Мыслительные операции, необходимые на этапе проектирования: действие по аналогии, анализ, обобщение.
1) Формула деления с остатком.
2) Алгоритм выделения целой части из неправильной дроби.
3) Знаковая форма выделения целой части из неправильной дроби.
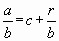
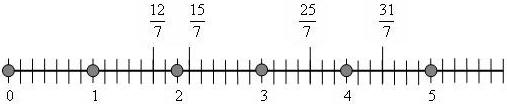
1) листочки с заданием (к этапу 2)
Опеределите по числовому лучу какому смешанному числу соостветствуют дроби
2) Подробный образец для самопроверки (к этапу 6)
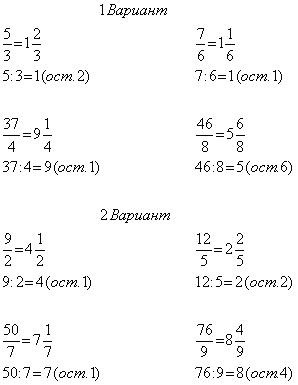
1 Самоопределение к учебной деятельности.
Цели:
- Мотивировать учащихся к учебной деятельности посредством закрепления ситуации успеха, достигнутой на предыдущем уроке.
- Определить содержательные рамки урока.
Организация учебного процесса на этапе 1.
— На протяжении нескольких уроков мы работали с некоторыми числами. С какими числами мы работали? (С дробными числами).
— Какие знания у нас есть об этих числах? (Умеем их читать, записывать, сравнивать, решать задачи).
— Предлагаю продолжить нашу плодотворную работу. Вы готовы? (Да).
— Сегодня мы продолжим работать с дробными числами. Я уверена, что у нас с вами все получится на отлично. Но сначала повторим материал предыдущих уроков.
2 Актуализация знаний и фиксация затруднений в индивидуальной деятельности.
Цели:
1. Актуализировать умение находить правильные и неправильные дроби, смешанные числа, определение правильной и неправильной дроби, смешанного числа.
2. Актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала.
3. Зафиксировать ситуацию, когда учащиеся не смогут выделить целую часть из неправильной дроби.
Организация учебного процесса на этапе 2.
— С какими числами мы познакомились на предыдущем уроке? (Со смешанными числами).
— Из чего состоит смешанное число? (Из целой и дробной части).
На доске записаны дроби и смешанные числа.
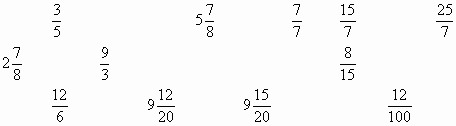
— На какие группы можно разделить представленные числа?
— Правильные дроби (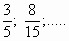 ).
).
— Какие дроби называются правильными? (Дробь, у которой числитель меньше знаменателя. Правильная дробь меньше единицы).
— Неправильные дроби. (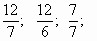 …..)
…..)
— Какие дроби называются неправильными? (Дробь, у которой числитель больше знаменателя или числитель равен знаменателю).
— Какие из неправильных дробей можно представить в виде натурального числа?
(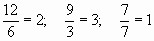 )
)
— Какую дробь можно представить в виде смешанного числа? (Неправильную дробь, где числитель больше знаменателя).
— Определите с помощью числового луча, какому смешанному числу равна дробь
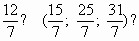
У учащихся лист с заданием (Р-1), один ученик работает у доски, комментирует.
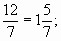
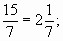
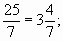
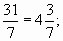
— Назовите наименьшее смешанное число?( 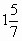 )
)
— Наибольшее? (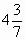 )
)
— Какое арифметическое действие вам помогло? ( Деление. Деление с остатком).
— Докажите. (На доске: Д-1).
— 12:7=1 (ост.5); 15:7=2 (ост.1); 25:7=3 (ост.4); 31:7=4 (ост.3)
— Выделите целую часть дроби 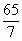 , запишите смешанное число. Дети работают на обратной стороне листочка. Разные варианты ответов выносятся на доску.
, запишите смешанное число. Дети работают на обратной стороне листочка. Разные варианты ответов выносятся на доску.
— Как вы действовали?
3 Выявление причин затруднения и постановка цели деятельности.
Цели:
- Организовать коммуникативное взаимодействие по выявлению отличительного свойства задания на выделение целой части из неправильной дроби.
- Согласовать тему и цель урока.
Организация учебного процесса на этапе 3.
— Какое задание вы выполняли? (Надо выделить целую часть из дроби 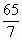 ).
).
— Чем это задание отличается от предыдущего? (Тот способ, который нам помогал выделять целую часть из неправильной дроби не подходит для дроби 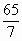 . Эту дробь неудобно показать на числовом луче).
. Эту дробь неудобно показать на числовом луче).
— Что же мы видим? (У нас получились разные ответы).
— Почему? (Мы пользовались разными способами. У нас нет алгоритма выделения целой части из неправильной дроби).
— Какова же цель нашего урока? (Построить алгоритм и научиться выделять целую часть из неправильной дроби).
— Подумайте и сформулируйте тему нашего урока. («Выделение целой части из неправильной дроби»).
На доске открывается название темы урока.
4 Построение проекта выхода из затруднения.
Цель:
- Организовать коммуникативное взаимодействие для построения нового способа действия для выделения целой части из неправильной дроби.
- Зафиксировать новый способ в знаковой и вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4
— 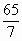 =?
=?
— Каким способом вы предлагаете найти, сколько в дробном числе целых единиц? (Числитель разделить на знаменатель).
— Какой знак в записи дроби вам подсказал, как надо действовать? (Черта дроби – знак деления).
числитель
разделить
на знаменатель
a : b
— Запишем дробь в виде частного: 65 : 7.
— Какой это вид деления? (Деление с остатком. На доске: Д-1).
— Найдите результат. (65 : 7 = 9) (ост. 2)
— Что означает в полученном равенстве частное 9 и остаток 2? (Частное 9 означает, что в 65 содержится 9 раз по 7 и 2 остается).
— Что будет обозначать частное 9 в смешанном числе? (9 – это целая часть смешанного числа).
частное ( c ) —
целая часть
— Что будет обозначать остаток 2 в смешанном числе? (2 – это числитель дроби смешанного числа).
остаток ( r ) —
числитель
— А знаменатель? (Он остается, не изменяется).
знаменатель ( b )
не изменяется
— Какое смешанное число у нас получилось?
— 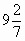
— Выполнили мы задание? (Да).
— Какое математическое действие нам помогло? (Деление с остатком. На доске: Д-1).
Учитель возвращается к ответам на листочках, обобщает, поощряет словом тех, кто выполнил правильно. В групповой форме учащиеся выводят новый способ в знаковой форме на листочках. Выбирается правильный вариант.
— Запишите, пользуясь формулой деления с остатком (Д-1), какому смешанному числу равна дробь 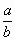 ?
?
— Как из неправильной дроби выделить целую часть?
— Чтобы выделить целую часть из неправильной дроби, надо её числитель разделить на знаменатель. Частное будет целой частью, остаток – числитель, а знаменатель не изменяется.
— Давайте всё же проверим наше мнение с мнением учебника. Откройте страницу 26, Математика 4 (2 часть), прочитайте правило сначала про себя, а потом вслух.
— Мы были правы? (Да).
Физминутка (по выбору учителя).
5 Первичное закрепление во внешней речи.
Цель:
Зафиксировать способ выделения целой части из неправильной дроби во внешней речи.
Организация учебного процесса на этапе 5.
— Давайте ещё раз повторим алгоритм выделения целой части из неправильной дроби. Д-2
— Мы с вами составили алгоритм выделения целой части из неправильной дроби. Какова цель нашей дальнейшей деятельности? (Потренироваться).
№ 4 (а,б,в) стр. 26 – с комментированием по образцу.
№ 4 (г, д) стр. 26 – в парах.
6 Самоконтроль с самопроверкой.
Цель:
- Организовать самостоятельное выполнение учащимися задания на выделение целой части из неправильной дроби.
- Тренировать способность к самоконтролю и самооценке.
- Проверить своё умение выделять целую часть из неправильной дроби.
- Способствовать созданию ситуации успеха.
Организация учебного процесса на этапе 6.
— Вы сумели вывести алгоритм выделения целой части из неправильной дроби и потренировались в решении примеров. Я думаю, теперь вы сможете выполнить задание сами.
№ 3 стр. 26 – 1 вариант – 1 и 2 столбик;
2 вариант – 3 и 4 столбик;
— Кто желает, может выполнить задание и другого варианта.
Учащиеся выполняют работу, по окончании которой проверяют себя по образцу для самопроверки. Используется карточка Р-2.
— Проверьте себя по образцу для самопроверки и зафиксируйте результат проверки при помощи знаков «+» или «?» зеленой ручкой.
— Кто допустил ошибки при выполнении задания? (…)
— У кого все верно?
Можно организовать работу по коррекции ошибок в группах или фронтально. Консультантами назначаются учащиеся, которые не допустили ошибок.
7 Включение в систему знаний и повторение.
Цель:
Тренировать способности выделять целую часть из неправильной дроби.
Организация учебного процесса на этапе 7.
— Попробуем применить наши знания при сравнении дроби и смешанного числа.
— Найдите неравенство, в котором надо сравнить правильную дробь с неправильной.
— 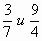
— Что будем делать?
— Выделим целую часть из неправильной дроби.
— 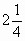 Значит?!
Значит?!
— 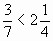
— Неправильная дробь больше правильной. Мы это доказали, выделив целую часть.
— Закончите задание, сравните.
8 Рефлексия учебной деятельности на уроке.
Цели:
- Зафиксировать в речи алгоритм выделения целой части из неправильной дроби.
- Зафиксировать затруднения, которые остались, и способы их преодоления.
- Оценить собственную деятельность на уроке.
- Согласовать домашние задание.
Организация учебного процесса на этапе 8.
— Чему научились на уроке? (Выделять целую часть из неправильной дроби).
— Какой алгоритм мы построили? (Можно проговорить алгоритм Д-2).
— У кого были трудности? Как будете, действовать?
— Кто сегодня доволен собой? Почему?
— Оцените объективно свою работу на уроке, выбрав соответствующее смешанное число. Число запишите зеленой ручкой на полях тетради.
— мне было трудно на уроке.
— я понял урок, но мне нужна тренировка.
— я хорошо понял урок, но нужна помощь.
— я молодец, понял урок на отлично.
Домашнее задание: придумать пять неправильных дробей и выделить целую часть; №10, №11 стр. 28 – по выбору; № 15 стр. 28 (а или б) – по желанию.

