Как построить поле корреляции в excel
Корреляцию в Excel можно найти по формуле:
Результат показан ниже
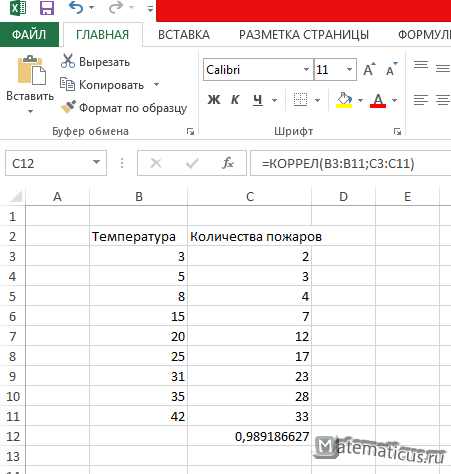
Также можно построить график поля корреляции
Для этого, переходим на вкладку Вставка в области диаграммы выбираем точечный график
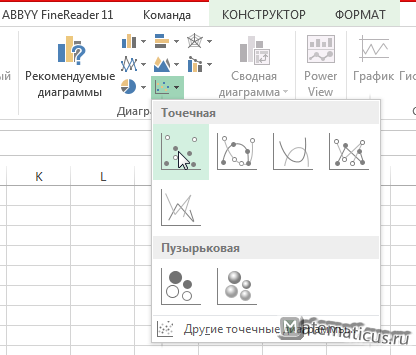
затем переходим на область графика
и выбираем данные из диапазона B3:C11, затем Ок. В итоги получаем график поля корреляции по точкам
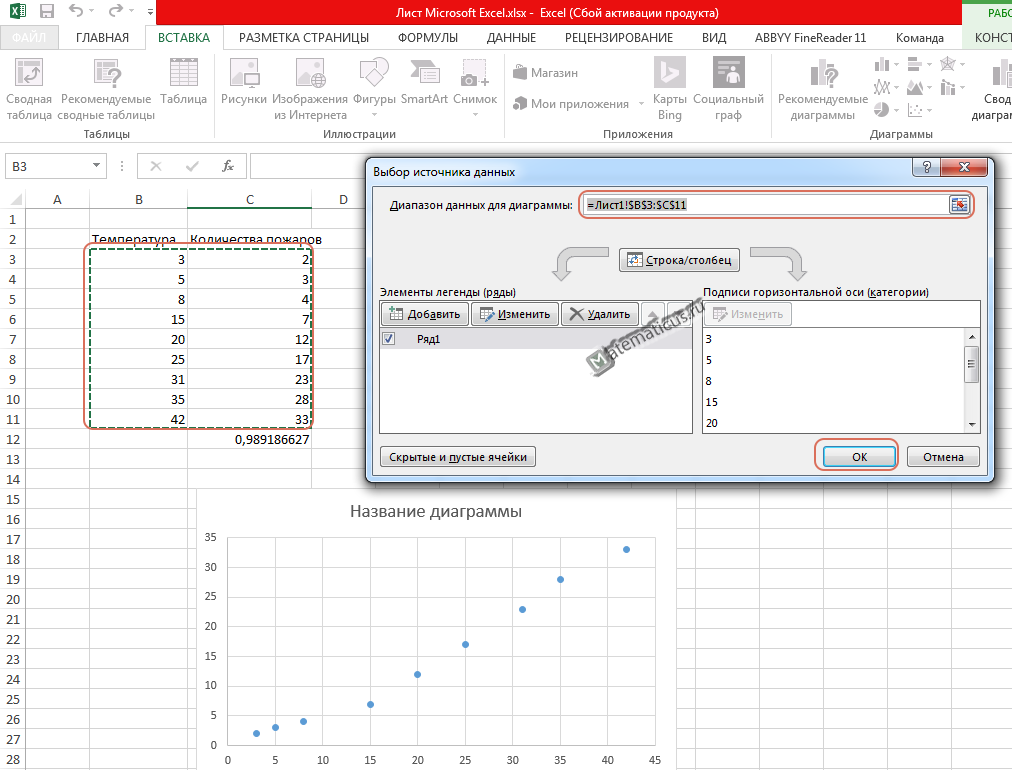
Также быстро корреляцию можно найти через анализ данных
Вкладка Данные, затем Анализ данных. Если у вас эта вкладка не отображается в Excel, то см. здесь как сделать надстройку.
Выбираем корреляцию и жмём Ок.
Такой же выбираем диапазон данных, как и ранее делали
В результате получаем отчёт

Аналитически, корреляция определяется по формуле:
Содержание отчета
2. Краткие теоретические сведения.
3. Порядок выполнения работы.
4. Исходные данные для разработки математической модели.
5. Результаты разработки математической модели.
6. Результаты исследования модели. Построение прогноза.
В задачах 2-4 можно использовать ППП Excel для расчетов характеристик модели.
Работа № 1.
Построение моделей парной регрессии. Проверка остатков на гетероскедастичность.
По 15 предприятиям, выпускающим один и тот же вид продукции известны значения двух признаков:
х — выпуск продукции, тыс. ед.;
у — затраты на производство, млн. руб.
| x | y |
| 5,3 | 18,4 |
| 15,1 | 22,0 |
| 24,2 | 32,3 |
| 7,1 | 16,4 |
| 11,0 | 22,2 |
| 8,5 | 21,7 |
| 14,5 | 23,6 |
| 10,2 | 18,5 |
| 18,6 | 26,1 |
| 19,7 | 30,2 |
| 21,3 | 28,6 |
| 22,1 | 34,0 |
| 4,1 | 14,2 |
| 12,0 | 22,1 |
| 18,3 | 28,2 |
Требуется:
1. Построить поле корреляции и сформулировать гипотезу о форме связи.
2. Построить модели:
Линейной парной регрессии.
Полулогарифмической парной регрессии.
2.3 Степенной парной регрессии.
Для этого:
Рассчитать параметры уравнений.
2. Оценить тесноту связи с помощью коэффициента (индекса)
корреляции.
3. Оценить качество модели с помощью коэффициента (индекса)
детерминации и средней ошибки аппроксимации.
4. Дать с помощью среднего коэффициента эластичности
сравнительную оценку силы связи фактора с результатом.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
По значениям характеристик, рассчитанных в пунктах 2-5 выбрать лучшее уравнение регрессии.
Используя метод Гольфрельда-Квандта проверить остатки на гетероскедастичность.
8. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Для уровня значимости  =0,05 определить доверительный интервал прогноза.
=0,05 определить доверительный интервал прогноза.
Строим поле корреляции.

Анализируя расположение точек поля корреляции, предполагаем, что связь между признаками х и у может быть линейной, т.е. у=а+bх, или нелинейной вида: у=а+blnх, у = ах b .
Основываясь на теории изучаемой взаимосвязи, предполагаем получить зависимость у от х вида у=а+bх, т. к. затраты на производство y можно условно разделить на два вида: постоянные, не зависящие от объема производства — a, такие как арендная плата, содержание администрации и т.д.; и переменные, изменяющиеся пропорционально выпуску продукции bх, такие как расход материала, электроэнергии и т.д.
2.1. Модель линейной парной регрессии.
2.1.1. Рассчитаем параметры a и b линейной регрессии у=а+bх.
В Excel имеется еще более быстрый и удобный способ построить график линейной регрессии (и даже основных видов нелинейных регрессий, о чем см. далее). Это можно сделать следующим образом:
1) выделить столбцы с данными X и Y (они должны располагаться именно в таком порядке!);
2) вызвать Мастер диаграмм и выбрать в группе Тип – Точечная и сразу нажать Готово ;
3) не сбрасывая выделения с диаграммы, выбрать появившейся пункт основного меню Диаграмма , в котором следует выбрать пункт Добавить линию тренда ;
4) в появившемся диалоговом окне Линия тренда во вкладке Тип выбрать Линейная ;
5) во вкладке Параметры можно активизировать переключатель Показывать уравнение на диаграмме , что позволит увидеть уравнение линейной регрессии (4.4), в котором будут вычислены коэффициенты (4.5).
6) В этой же вкладке можно активизировать переключатель Поместить на диаграмму величину достоверности аппроксимации (R^2) . Эта величина есть квадрат коэффициента корреляции (4.3) и она показывает, насколько хорошо рассчитанное уравнение описывает экспериментальную зависимость. Если R 2 близок к единице, то теоретическое уравнение регрессии хорошо описывает экспериментальную зависимость (теория хорошо согласуется с экспериментом), а если R 2 близок к нулю, то данное уравнение не пригодно для описания экспериментальной зависимости (теория не согласуется с экспериментом).
В результате выполнения описанных действий получится диаграмма с графиком регрессии и ее уравнением.
§4.3. Основные виды нелинейной регрессии
Параболическая и полиномиальная регрессии.
Параболической зависимостью величины Y от величины Х называется зависимость, выраженная квадратичной функцией (параболой 2-ого порядка):
Это уравнение называется уравнением параболической регрессии Y на Х . Параметры а , b , с называются коэффициентами параболической регрессии . Вычисление коэффициентов параболической регрессии всегда громоздко, поэтому для расчетов рекомендуется использовать компьютер.
Уравнение (4.8) параболической регрессии является частным случаем более общей регрессии, называемой полиномиальной. Полиномиальной зависимостью величины Y от величины Х называется зависимость, выраженная полиномом n -ого порядка:
где числа а i (i =0,1,…, n ) называются коэффициентами полиномиальной регрессии .
Степенной зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением степенной регрессии Y на Х . Параметры а и b называются коэффициентами степенной регрессии .
Это уравнение описывает прямую на плоскости с логарифмическими координатными осями lnx и ln . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки логарифмов эмпирических данных lnx i и lnу i находились ближе всего к прямой (4.11).
Показательной (или экспоненциальной ) зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением показательной (или экспоненциальной ) регрессии Y на Х . Параметры а (или k ) и b называются коэффициентами показательной (или экспоненциальной ) регрессии .
Если прологарифмировать обе части уравнения степенной регрессии, то получится уравнение
Это уравнение описывает линейную зависимость логарифма одной величины ln от другой величины x . Поэтому критерием применимости степенной регрессии служит требование того, чтобы точки эмпирических данных одной величины x i и логарифмы другой величины lnу i находились ближе всего к прямой (4.13).
Логарифмической зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением логарифмической регрессии Y на Х . Параметры а и b называются коэффициентами логарифмической регрессии .
Гиперболической зависимостью величины Y от величины Х называется зависимость вида:
Это уравнение называется уравнением гиперболической регрессии Y на Х . Параметры а и b называются коэффициентами гиперболической регрессии и определяются методом наименьших квадратов. Применение этого метода приводит к формулам:
В формулах (4.16-4.17) суммирование проводится по индексу i от единицы до количества наблюдений n .
К сожалению, в Excel нет функции, вычисляющих коэффициенты гиперболической регрессии. В тех случаях, когда заведомо не известно, что измеряемые величины связаны обратной пропорциональностью, рекомендуется вместо уравнения гиперболической регрессии искать уравнение степенной регрессии, так в Excel имеется процедура ее нахождения. Если же между измеряемыми величинами предполагается гиперболическая зависимость, то коэффициенты ее регрессии придется вычислять с помощью вспомогательных расчетных таблиц и операций суммирования по формулам (4.16-4.17).
Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ .
Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.
Основными типами нелинейных регрессий являются:
- полиномиальные (квадратичная, кубическая);
- гиперболическая;
- степенная;
- показательная;
- логарифмическая.
Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.
В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А ), если она находится в промежутке Категории: / / от 28.10.2017
Известна тем, что она полезна в разных областях деятельности, включая и такую дисциплину, как эконометрика, где в работе используется данная программная утилита. В основном все действия практических и лабораторных занятий выполняют в Excel, которая существенно облегчает работу, давая подробные объяснения тех или иных действий. Так, один из инструментов анализа «Регрессия» применяется с целью подбора графика для набора наблюдений за счет метода наименьших квадратов. Рассмотрим, что представляет собой данный инструмент программы и в чем заключается его польза для пользователей. Ниже также предоставлена краткая, но понятная инструкция построения регрессионной модели.
Основные задачи и виды регрессии
Регрессия представляет собой зависимость между заданными переменными, за счет чего можно определить прогноз будущего поведения данных переменных. Переменные — это различные периодические явления, включая и поведение человека. Такой анализ программы Excel применяется для того, чтобы проанализировать воздействие на конкретную зависимую переменную значений одной или некоторым количеством переменных. К примеру, на продажи в магазине влияет несколько факторов, включая ассортимент, цены и место локализации магазина. Благодаря регрессии в Excel можно определять степень влияния каждого из указанных факторов по результатам имеющихся продаж, а после применить полученные данные для прогнозирования продаж на другой месяц или для другого магазина, расположенного рядом.
Обычно регрессия представлена в виде простого уравнения, раскрывающего зависимости и силу связи между двумя группами переменных, где одна группа является зависимой или эндогенной, а другая — независимой или экзогенной. При наличии группы взаимосвязанных показателей зависимая переменная Y определяется исходя из логики рассуждений, а остальные выступают в роли независимых Х-переменных.
Основные задачи построения регрессионной модели заключаются в следующем:
- Отбор значимых независимых переменных (Х1, Х2, …, Xk).
- Выбор вида функции.
- Построение оценок для коэффициентов.
- Построение доверительных интервалов и функции регрессии.
- Проверка значимости вычисленных оценок и построенного уравнения регрессии.
Регрессионный анализ бывает нескольких видов:
- парный (1 зависимая и 1 независимая переменные);
- множественный (несколько независимых переменных).
Уравнения регрессии бывает двух видов:
- Линейные, иллюстрирующие строгую линейную связь между переменными.
- Нелинейные — уравнения, которые могут включать степени, дроби и тригонометрические функции.
Инструкция построения модели
Чтобы выполнить заданное построение в Excel, необходимо следовать указаниям:

Для дальнейшего вычисления следует использоваться функцию «Линейн ()», указывая Значения Y, Значения Х, Конст и статистику. После этого определите множество точек на линии регрессии с помощью функции «Тенденция» — Значения Y, Значения Х, Новые значения, Конст. При помощи заданных параметров вычислите неизвестное значение коэффициентов, опираясь на заданные условия поставленной задачи.
Тема: КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
ЛАБОРАТОРНАЯ РАБОТА №1
1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИ В ПРОГРАММЕ EXCEL
Корреляционная связь — это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений.
Парная корреляция — это связь между двумя показателями, один из которых является факторным, а другой — результативным.
Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.
Необходимые условия применения корреляционного анализа:
1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей.
2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.
Применение корреляционного анализа позволяет решить следующие задачи:
1.Определить изменение результативного показателя под воздействием одного или нескольких факторов.
2. Установить относительную степень зависимости результативного показателя от каждого фактора.
Имеются данные по 20 сельскохозяйственным хозяйствам. Найти коэффициент корреляции между величинами урожайности зерновых культур и качеством земли и оценить его значимость. Данные приведены в таблице.
Таблица. Зависимость урожайности зерновых культур от качества земли
Качество земли, балл х
Урожайность, ц/га у
Для нахождения коэффициента корреляции использовать функцию КОРРЕЛ .
Значимость коэффициента корреляции проверяется по критерию Стьюдента .
Для рассматриваемого примера r=0,99, n=18.
Для нахождения квантиля распределения Стьюдента используется функция СТЬЮДРАСПОБР со следующими аргументам: Вероятность –0,05, Степени свободы –18.
Сравнив значение t-статистики с квантилем распределения Стьюдента сделать выводы о значимости коэффициента парной корреляции. Если расчетное значение t-статистики больше квантиля распределения Стьюдента, то величина коэффициента корреляции является значимой.
ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ МЕЖДУ ДВУМЯ ВЕЛИЧИНАМИ
По данным задания 1:
1) построить уравнение регрессии (линейную модель), которое характеризует прямолинейную зависимость между качеством земли и урожайностью;
2). выполнить проверку адекватности полученной модели.
1. На листе Excel выделить массив свободных ячеек из пяти строк и двух столбцов.
2. Вызвать функцию ЛИНЕЙН .
3.Указать для функции следующие аргументы: Изв_знач_ y Урожайность, ц/га; Изв_знач_ x — столбец значений показателя Качество земли, балл ; Константа –1, Стат– 1 (позволяет вычислить показатели, используемые для проверки адекватности модели. Если Стат– 0, то такие показатели вычисляться не будут.
4. Нажать комбинацию клавиш Ctrl — Shift — Enter .
В выделенные ячейки выводятся коэффициенты модели, а также показатели, позволяющие проверить модель на адекватность (таблица 2).

