Как построить график в полярной системе координат
Полярная система координат состоит из заданной фиксированной точки O, называемой полюсом, концентрических окружностей с центром в полюсе и лучей, выходящих из точки O, один из которых OX – полярная ось.
Расположение любой точки M в полярных координатах можно задать положительным числом ρ=|ОМ|, равным расстоянию от полюса до точки, и числом φ, равным величине угла ХОМ (полярный угол). ρ и φ называют полярными координатами точки M, и точку обозначают M(ρ, φ). Для формирования графика в полярных координатах используется функция polar(φ, ρ, s),где φ — массив полярных углов, ρ — массив значений полярных радиусов точек, образующих графики.
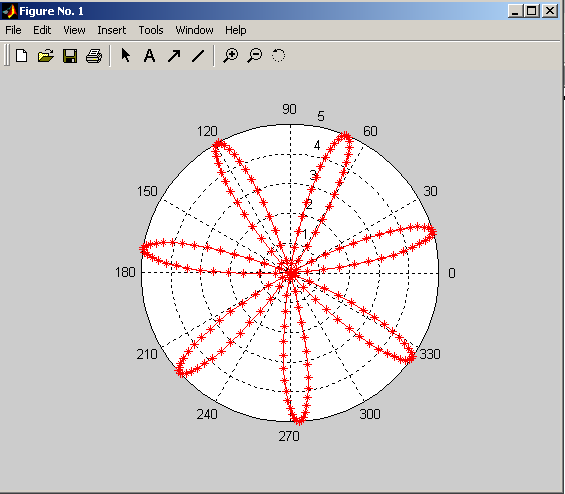
Пусть требуется построить график функции r(φ)=5cos(2-7φ). При построении графика функции в полярных координатах будем изменять аргумент от до 2.
Необходимо сформировать массивы значений полярного угла φ и полярного радиуса r (аргументом является угол) r(φ)=5cos(2-7φ).
Можно также указать тип и цвет линий, тогда :
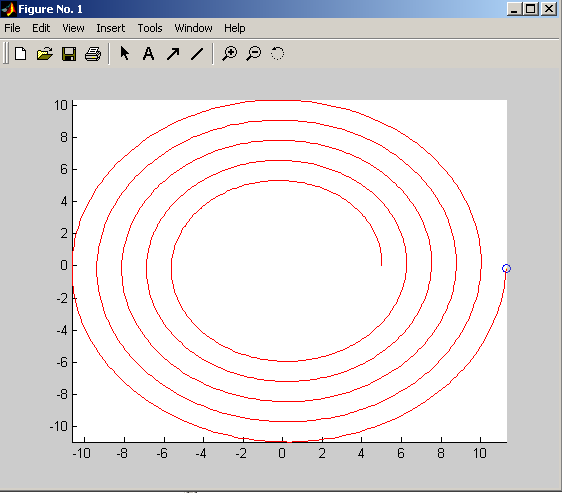
Для построения траектории движения точки на плоскости (анимация) предусмотрена функция comet, а для построения траектории движения точки в трехмерном пространстве – функция comet3. Это простой способ создать анимированное изображение.
Изобразим движение точки по траектории, заданной параметрически.
Построим траекторию движения точки в пространстве.
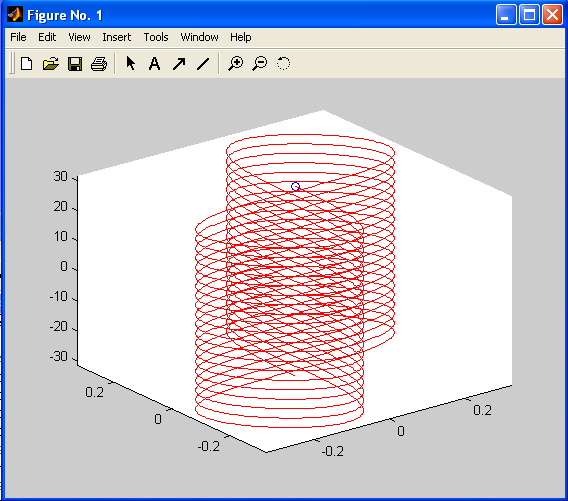
Для более сложной анимации можно использовать команды getframe и movieview. Команда getframe захватывает активное окно изображения в один кадр фильма, а команда movieview воспроизводит результат в отдельном окне. Приведенные ниже команды воспроизводят кадры с вибрирующей струной:
В приведенном выше примере для организации цикла используется оператор for, работа которого будет описана далее.
Трехмерная графика.
График поверхности (трехмерный график) – это график, положение точки в котором определяется значениями трех координат. Трехмерным аналогом функции plot является функция plot3, которая позволяет создавать трехмерные линии. Если есть три вектора x, y, z, задающих координаты точек в трехмерном пространстве, то при выполнении функции plot3(x,y,z), построится трехмерная линия на плоскости.
Пусть требуется построить график линии, заданной формулами:
Построилась винтовая линия (спираль).
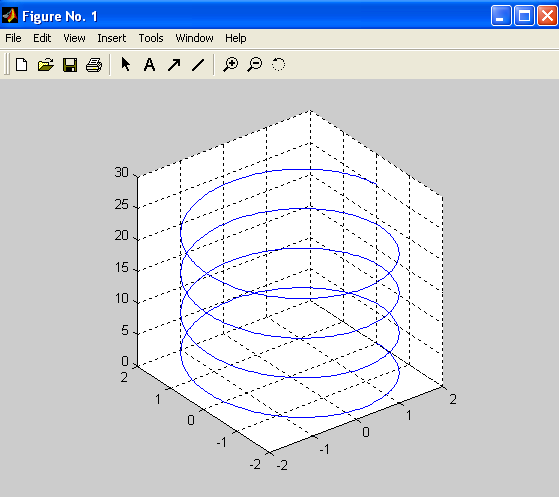
Функция plot3, также как и функция plot, может иметь дополнительный аргумент, задающий параметры линии (тип линии, цвет и тип маркера). Например, plot3(x,y,z, ‘g*’).
Можно также использовать команду ezplot3:
Для вычерчивания каркасных поверхностей в трехмерном пространстве существуют две основные функции: mesh и surf.
Команда mesh(Z) – строит прозрачную сетчатую поверхность, а команда surf(Z)- затененную, где Z — матрица, значения элементов которой определяют соответствующие координаты на графике. Построим прозрачную поверхность для единичной матрицы, задав команды:
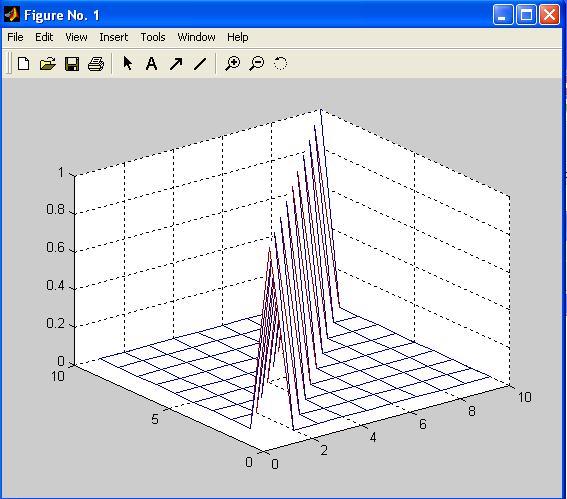
По главной диагонали расположены “пики” – единицы.
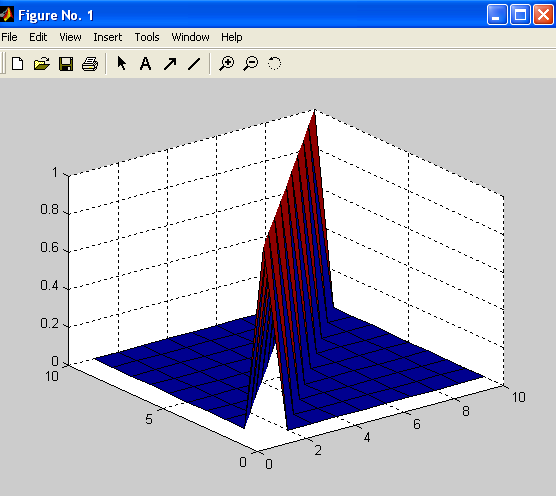
Аналогично, задав команду:
Получим затененную поверхность.
Для построения в трехмерном пространстве функции от 2-х переменных Z(X, Y) необходимо сначала с помощью векторов x и y задать прямоугольную сетку, которая будет использоваться как основание для построения трехмерной поверхности. Для этого надо воспользоваться функцией meshgrid, которая создает эту сетку из точек в прямоугольной области с заданными интервалами. Диапазоны значений по осям x и y задаются векторами x и y соответственно. Имена векторов и матриц могут различаться.
Пусть значения по осям x и y заданы векторами x и y:
Сформируем матрицы X и Y с помощью функции meshgrid:
На основе векторов x и y формируются две матрицы, в которые записываются координаты узлов сетки. Матрица X содержит одинаковые строки, в которых заданы координаты X. Матрица Y содержит одинаковые столбцы, в которых заданы координаты Y. Наложение матриц X и Y позволяет получить пары (xi и yj), для которых в дальнейшем вычисляется значение функции Z. Значения функции в узлах сетки записываются в матрицу Z, размерность которой равна размерности матриц X и Y.
Построим график функции, которая имеет вид:
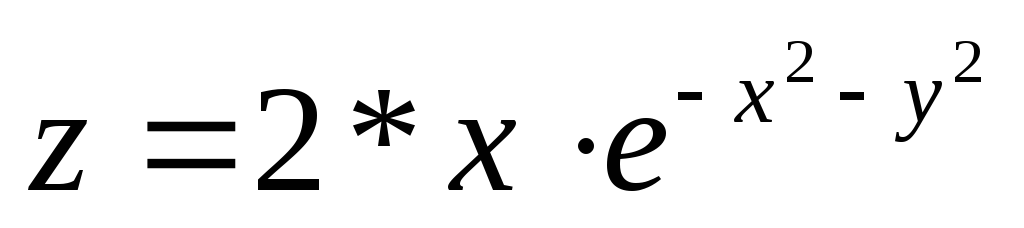 на заданном интервале от-2 до 2 и от y от -4 до 4 с шагом равным 0.1
на заданном интервале от-2 до 2 и от y от -4 до 4 с шагом равным 0.1
Зададим два вектора x и y, используя запись:
если оба вектора одинаковые, то можно записать: y= x
Далее вызывается команда
Значения векторов можно указать прямо внутри команды meshgrid(-2:0.1:2,-4:0.1:4)
Создаётся прямоугольная сетка с шагом 0.1, которая используется для построения 3-х мерной поверхности. Каждому значению x ставится в соответствие каждое значение y. Для каждой пары xi yi,,(в узлах сетки) будет вычислено значение функции Z. В результате сформируется матрица из вычисленных значений функции. После этого можно вызвать команду для вывода изображения на экран.
Ниже приведен пример построения графика с использованием функции plot3:
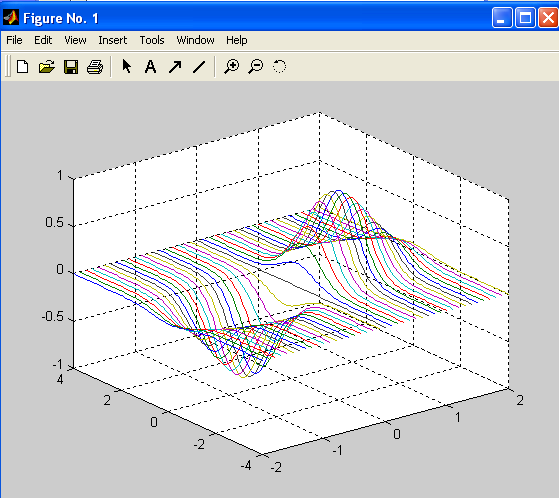
Более наглядные графики получаются с использованием функции mesh.
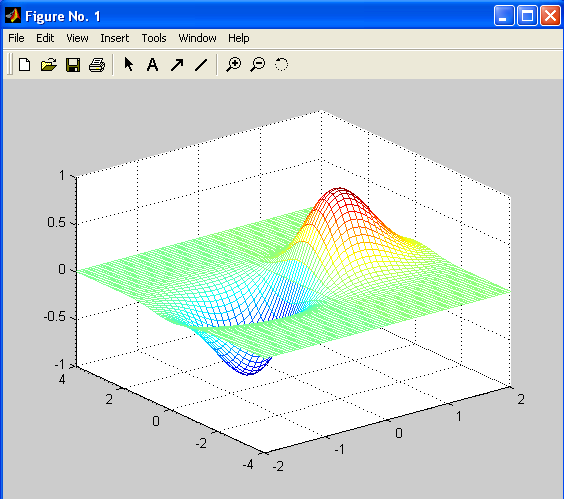
Линии на разных участках графика окрашены в разные цвета. Эти цвета соответствуют значениям функции. По умолчанию оттенки красного цвета соответствуют большим значениям функции, а синего – меньшим.
Можно сделать “прозрачной” каркасную поверхность, отобразив ее скрытые части, применив команду hidden off. Отмена — hidden on.
Если использовать функцию meshz(X,Y,Z), то будет видно основание, на котором построен график.
Введите график функции
Важно phi должно лежать в правильном промежутке, иначе график не сможет построиться
Построим график функции в полярных координатах r=r(φ),
где Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x|) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x e e число, которое примерно равно 2.7 exp(x) Функция — экспонента от x (что и e^x) log(x) or ln(x) Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) pi Число — "Пи", которое примерно равно 3.14 sin(x) Функция — Синус от x cos(x) Функция — Косинус от x sinh(x) Функция — Синус гиперболический от x cosh(x) Функция — Косинус гиперболический от x sqrt(x) Функция — квадратный корень из x sqr(x) или x^2 Функция — Квадрат x tg(x) Функция — Тангенс от x tgh(x) Функция — Тангенс гиперболический от x cbrt(x) Функция — кубический корень из x floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) sign(x) Функция — Знак x erf(x) Функция ошибок (Лапласа или интеграл вероятности)
© Контрольная работа РУ — калькуляторы онлайн
В простейших случаях допустимо строить график функции, заданной в полярных координатах, по точкам (см. пример занятия 15).
Построение графика функции ρ=f(  в общем случае осуществляется так: а) строят для функции ρ=f(
в общем случае осуществляется так: а) строят для функции ρ=f(  соответствующую функцию y=f(x); б) исследуют функцию ρ=f(
соответствующую функцию y=f(x); б) исследуют функцию ρ=f(  , сравнивая ее с соответствующей функцией y=f(x), учитывая отмеченные выше особенности графика функции ρ=f(
, сравнивая ее с соответствующей функцией y=f(x), учитывая отмеченные выше особенности графика функции ρ=f(  ; в) выполняют построение графика функции ρ=f(
; в) выполняют построение графика функции ρ=f(  по графику функции y=f(x).
по графику функции y=f(x).
Ограниченность функции.
Если функция y=f(x) ограничена (M 0, а затем строить кривую ρ=f(  для
для  , соответствующих значениям х, при которых f(x)
, соответствующих значениям х, при которых f(x)

 =
= 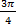 эти значения равны 3 и -3.
эти значения равны 3 и -3.
Функция y=3sin2  при x
при x  ]0;
]0;  [
[ 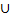 ]
] 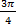 ;
; 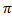 [ возрастающая при x
[ возрастающая при x  ]
]  ;
;  [
[ 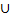 ]
]  ;
; 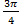 [ убывающая; соответственно, функция, ρ=3sin2
[ убывающая; соответственно, функция, ρ=3sin2  возрастающая при
возрастающая при 
 ]
]  ;
;  [
[ 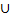 ]
]  ;
; 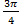 [. Кривая y=3sin2
[. Кривая y=3sin2  асимптот не имеет, не имеет их и кривая ρ=3sin2
асимптот не имеет, не имеет их и кривая ρ=3sin2  . Следовательно, кривая ρ=3sin2
. Следовательно, кривая ρ=3sin2  располагается в круге радиусом 3 с центром в полюсе.
располагается в круге радиусом 3 с центром в полюсе.
Учитывая симметрию кривой ρ=3sin2  относительно полюса и ее периодичность, строим кривую ρ=3sin2
относительно полюса и ее периодичность, строим кривую ρ=3sin2  для 0≤
для 0≤  ≤
≤  . Это построение выполняем так: сначала строим точку экстремума
. Это построение выполняем так: сначала строим точку экстремума
A1(  ) и точки, для которых ρ = 0: A2(
) и точки, для которых ρ = 0: A2(  ), A1(
), A1(  ); после этого строим точки B1(ρ;
); после этого строим точки B1(ρ;  ), B2(ρ;
), B2(ρ; 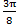 ) .
) .
Заметим, что значения ρ для точек B1 и B2 получим из графика функции y=3sin2  , взяв соответствующую ординату кривой для точек х=
, взяв соответствующую ординату кривой для точек х=  и х=
и х=  . Аналогично строим точки С1 и С2 . Проведя через эти точки линию, получим график функции ρ=3sin2
. Аналогично строим точки С1 и С2 . Проведя через эти точки линию, получим график функции ρ=3sin2  для 0≤
для 0≤  ≤
≤  (рис 298, а). Учитывая симметрию относительно полюса, строим кривую ρ=3sin2
(рис 298, а). Учитывая симметрию относительно полюса, строим кривую ρ=3sin2  для —
для —  ≤
≤  ≤0 (рис 298, б). Наконец, с помощью поворота на угол
≤0 (рис 298, б). Наконец, с помощью поворота на угол  вокруг полюса получаем график функции ρ=3sin2
вокруг полюса получаем график функции ρ=3sin2  (рис 298 в).
(рис 298 в).

- ρ=αcos2
 (четырехлепестковая роза)
(четырехлепестковая роза)
Воспользовавшись формулой cos2  =sin(
=sin(  +2
+2  ) приведем заданную функцию к виду
) приведем заданную функцию к виду
ρ =αsin(  +2
+2  ).
).
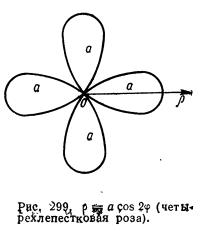 |
Очевидно, что график функции ρ =αsin(  +2
+2  ) получим из графика функции ρ=αcos2
) получим из графика функции ρ=αcos2  с помощью поворота на
с помощью поворота на 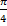 (рис 299)
(рис 299)
- ρ=
 , или ln ρ=α
, или ln ρ=α 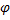 (логарифмическая спираль), α>0
(логарифмическая спираль), α>0 - ρ =
 ,
, 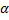 >0.
>0. - ρ =
 b (конхоида)
b (конхоида)
Занятие 17.
Тема занятия: «Контрольная работа № 2.»
План занятия.
1. Контрольная работа № 2.
Методические материалы.
Содержит задачи из разделов: "Основные тригонометрические функции и обратные тригонометрические функции", "Преобразование тригонометрических выражений", "Показательная функция. Показательные уравнения и неравенства", "Логарифмическая функция. Логарифмические уравнения и неравенства", "Производная. Геометрический смысл. Производная сложной функции", "Исследование функций одной переменной".
Контрольные мероприятия
Перед проведением текущих аттестаций выполняются контрольные работы. Контрольные работы направлены на выявление практических навыков в решении задач элементарной математики по рассмотренным темам и усвоения нового материала. Представляют собой билет с 5 задачами.
Контрольная работа № 1.
Планируется на 7 занятии. На ее выполнение отводится 1 час времени.
Контрольная работа № 2.
Планируется на последнем занятии. На ее выполнение отводится 1 час времени.
Требования при подведении итогов текущей и промежуточной аттестаций, определяющие условия, при которых цикл практических занятий считается зачтенным
Дисциплина состоит из курса с практическими занятиями, завершающегося зачетом.
Знания студентов по дисциплине оцениваются по 100-бальной системе со следующими диапазонами баллов:
| Зачет | Не зачтено | Зачтено | ||
| Академическая оценка (по 4-бальной системе) | Неудовлет-ворительно | Удовлет-ворительно | Хорошо | Отлично |
| Бальная оценка (по 100-бальной системе) | От 0 до 39 включи-тельно | От 40 до 60 вклю-чительно | Свыше 60 до 80 вклю-чительно | Свыше 80 до 100 вклю-чительно |
Бальная оценка по дисциплине определяется как сумма баллов, набранных студентом в результате работы в семестре (текущая успеваемость, 60 баллов) и на зачете (промежуточная аттестация, 40 баллов).
Бальная оценка текущей успеваемости складывается из следующих показателей:
· посещаемость — 0-10 баллов (0-5 баллов на каждую аттестацию);
· выполнение контрольной работы № 1 — 0-15 баллов,
· выполнение контрольной работы № 2 — 0-15 баллов,
· выполнение домашних заданий — 0-20 баллов (0-10 баллов на каждую аттестацию).
Отчеты по выполнению самостоятельной работы (домашних заданий) сдаются на проверку дважды в семестре: первый отчет не позднее 31 октября (дня текущей аттестации), второй отчет не позднее зачетной недели. Студенты, не сдавшие отчеты по самостоятельной работе, не допускаются к промежуточной аттестации.
Практические занятия к текущей аттестации будет зачтены при условии выполнения домашних заданий, что подтверждается сдачей отчета по домашним заданиям и набранной балльной оценки не менее 10 баллов.
Цикл практических занятий за семестр считается зачтенным при условии выполнения контрольных работ и сдачи отчетов, содержащих домашние задания.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: Учебник для вузов. В 3 т. Т.1. — М.: Невский диалект, 2001 .— 680 с.; Т.2. — М.: Невский диалект, 2006 .— 864 с.
2. Кремер Н.Ш., Константинова О.Г., Фридман М.Н. Математика для поступающих в экономические вузы: Учеб. пособие / Под ред. Н.Ш.Кремера. — М.: Юнити-Дана, 2004 .— 605с.
1. Выгодский М.Я. Справочник по элементарной математике. — М.: АСТ: Астрель, 2008.— 509 с.
2. Золотухин А.Я. Элементы теории множеств, меры и интеграла Лебега. Тула: ТулГУ, 2007. – 107с.
3. Иванов К.П. Сборник задач по элементарной математике для абитуриентов. — СПб.: Невский Диалект, 2007. — 336 с.
4. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). СПб.: Лань, 2008. – 240 с.
5. Симонян, А.З. Математика : Метод.пособие для поступающих в ТулГУ / Симонян А.З.;ТулГУ .— Тула, 2006 .— 112с.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

