Как называется процесс факторизации модуля проекта по

Проблема факторизации чисел возникла не вчера, она насчитывает тысячелетия. Можно лишь гадать почему в 1900 г на Математическом конгрессе Д. Гильберт не включил ее в список своих 23 проблем, а позднее она не попала в список нерешенных математических задач С. Улама. Особое внимание и интерес математиков к проблеме обозначился лишь в последние десятилетия. Возможно, стимулом стало открытие нового направления — двухключевой криптологии, появление шифров с открытым ключом. Можно предположить, что сегодняшний интерес к проблеме факторизации чисел продиктован некоторой неопределенностью относительно теоретического обоснования стойкости к раскрытию весьма популярного сегодня двухключевого шифра (личного ключа) RSA, который в принципе может быть взломан и без знания закрытого ключа. Бесключевое дешифрование. Просто в теории алгебраических колец до сих пор не найдены необходимые для этого результаты. Но есть не менее важный аспект этой проблемы — отсутствие операции обратной к умножению чисел. Простое быстрое и доступное мультипликативное разложение составных чисел может стать такой арифметической операцией, и пополнит арсенал вычислительных средств математики.

Краткое описание современной ситуации в области факторизации

Дабы прояснить ситуацию сегодняшнего дня в области факторизации натуральных чисел (элементов натурального ряда чисел (НРЧ)) и оценить возможности современного уровня ее разрешения фирмой RSA в 1991 г. был сформирован и опубликован список из 42 тестовых чисел различной разрядности от 100 до 617 десятичных цифр, позднее получивших название RSA-чисел. Фирмой было предложено всем желающим попробовать свои силы и использовать математическую подготовку в решении задачи факторизации больших чисел (ЗФБЧ) из этого списка. Для стимулирования активности участников за каждое факторизованное число была назначена премия. В условиях такого конкурса оговаривалось, что все числа списка получены путем перемножения лишь двух простых чисел практически одинаковой разрядности и, что разность этих сомножителей имеет разрядность такого же порядка (т.е. числа не близкие одно другому). «Конкурс» растянулся на два с лишним десятилетия и пока не завершен (список чисел не разложен). Возможно «конкурс» будет продолжен еще не на одно десятилетие. К настоящему времени опубликованы результаты разложения всего 13 первых чисел списка. Наибольшее из них описывается 232-мя десятичными цифрами, сомножители образованы 116-ю цифрами. Публикация об этом 2010 года.

Таблица 1 – Достижения в области факторизации больших чисел (модулей сравнения шифра RSA), список которых объявлен фирмой RSA в 1991 году.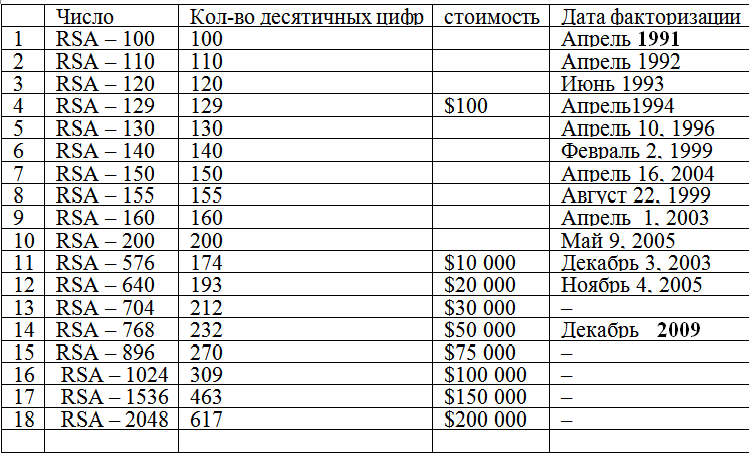

Анализ почти 20-летних усилий и результатов успешной факторизации RSA-чисел позволяет сделать вывод о том, что методы, используемые коллективами и отдельными математиками при решении ЗФБЧ, существенным образом зависят от такого свойства факторизуемого числа как его длина. Чем длиннее число, тем больше лет требовалось для его факторизации.
Спустя 10-15 лет представители фирмы перестали беспокоиться по поводу скорого краха, спокойно и успешно функционируют по сей день. Так в финансовом отчете фирмы за 2003 год говорилось о реализации на рынке ≈500 млн копий программ шифрования. Стойкость шифра к взлому обеспечивается невозможностью за приемлемое для практики (часы, сутки) время решить ЗФБЧ. Это подтверждается многолетними попытками факторизации чисел из списка и исследованиями в этой области. Но при этом не отрицается, что при изобретении более совершенного алгоритма решения ЗФБЧ или какого-либо другого атакующего алгоритма (например, бесключевого дешифрования) шифр не устоит.
Если принцип алгоритмизации решения ЗФБЧ останется прежним, то фирма простым увеличением длины ключа продлит жизненный цикл шифра, быстродействие которого, конечно, будет хуже, но останется приемлемым для части пользователей.
В этой работе не будут рассматриваться алгоритмы, решающие ЗФБЧ годами. Скажем только, что все они используют идеи числовых решет, начиная от решета Эратосфена, затем Бруна, Сельберга, Линника, Ленстры и т.п… Эти алгоритмы последовательно во времени модифицируются и совершенствуются на протяжении десятилетий, а «воз и ныне там». Привлечение теории эллиптических кривых несколько улучшает ситуацию, но к коренному перелому ситуации не приводит.
Считаю названное направление и подход в целом тупиковым. Повышение быстродействия вычислителей, распараллеливание процессов в рамках сохраняющегося принципа ситуацию не улучшит. Просто решение станет более дорогим.

Мотивация нового подхода

Перспективный выход из сложившегося положения видится таким. Необходимо совместно рассматривать число и окружающую его область, совместно разрабатывать математические алгоритмы решения ЗФБЧ на основе свойств факторизуемых чисел и числовой системы, которые были бы свободны от разрядности чисел, не зависели от их длины. Свойства числовой системы при этом нельзя игнорировать, что достаточно наглядно демонстрирует открытый автором «Закон распределения делителей в НРЧ». Это новый теоретический фундаментальный результат. Закон распределения делителей. Закон указывает для любого составного нечетного натурального числа (сннч), где в ограниченной области НРЧ лежат его делители или кратные им числа. Только при выполнении названных условий алгоритм сможет обеспечить высокое быстродействие, и время t получения решения не будет зависеть от длины числа N.
Подтверждением потенциальных возможностей таких алгоритмов служат широко известные признаки делимости чисел. Так, свойство числа иметь свертку s(N) – сумму цифр числа, кратную трем не зависит от его длины или зависимость эта очень слабая. Числа произвольной длины с таким свойством на ПК делятся на 3 практически мгновенно. Другие свойства, называемые признаками делимости, используемые при факторизации N, обеспечивают успешное решение нахождение частных разложений. К сожалению, известные в настоящее время свойства чисел и их систем не обеспечивают полного решения проблемы. С другой стороны, они демонстрируют возможности практически мгновенно в частных случаях проблему факторизации закрыть. В этом я вижу один из намеков нам со стороны числовой системы, на скрытые пока от нас возможности решения ЗФБЧ. Другой намек — бесключевое дешифрование. Периодичность появления исходного текста очевидна, ищите период.
Отсюда возникает потребность и необходимость поиска новых свойств, свободных от длины числа и использование их при разработке алгоритмов факторизации. Примером такого нового свойства является найденный автором новый ф-инвариант числа Новый инвариант числа.

Моделирование и базис исследований

В большинстве математических исследований объектов важную роль играют математические модели объектов. Разработка таких моделей для отдельного числа и их системы (НРЧ) представляет самостоятельное направление в исследованиях. Автором в опубликованных работах предложено несколько различных моделей и НРЧ, и отдельных натуральных чисел.
Читателю (не боги горшки обжигают), желающему всерьез заняться (не на коленке, как написал один из комментаторов) проблемой факторизации чисел, а возможно и других объектов (матриц, многочленов …), излагаемые в работах подходы к моделированию окажут существенную помощь и могут служить начальными примерами.
Где сегодня можно почитать о распределении делителей натурального числа в НРЧ? Кто из известных математиков публиковал материалы об этом? Где в НРЧ могут находиться простые числа, а где нет? Область запрета. Как можно моделировать натуральный ряд? Как устроены числа НРЧ? Классы чисел
Эти и другие вопросы возникали у автора, на которые приходилось искать ответы, перелопачивая можно сказать, горы литературы от Н. Бурбаки и многотомных энциклопедий до учебных пособий творчески работающих авторов. На ряд вопросов ответы найти пока не удалось, а на некоторые пришлось ответы творить самостоятельно. Что-то удалось строго доказать, что-то остается на уровне гипотез.
Возможно, не всем читателям представленные результаты покажутся интересными и важными. Автор убежден тому, кому это интересно, результаты будут весьма полезны. Думаю, что пока почитать об этом больше просто негде. Это новые и оригинальные результаты. Кто в состоянии быть объективным может это увидеть и оценить.
В цикле опубликованных работ излагается определенный базис знаний в четко определенной области: НРЧ и его элементы. После этих публикаций мои ученики получили возможность более основательно познакомиться с тем материалом, который им излагался устно, или вообще не доводился. Среди учеников люди с разным уровнем подготовки есть школьники, студенты, выпускники ВУЗов, специалисты со степенями и с учеными званиями. В первую очередь для меня имеют значение их реакция на текст и их вопросы к автору. В нашей жизни есть вещи важнее рейтингов и кармы, а в целом я Хабру благодарен за предоставленную возможность поместить у него свои тексты.

О форме и стиле изложения текстов

В комментариях к моим работам читателями высказывались замечания, пожелания, советы и критика. Благодарю всех за внимание к работам. Я не программист (не кодирую алгоритмы в языках высокого уровня), не IT- шник. Пишу как считаю нужным и учусь оформлению. Стиль изложения работ мной выбран сознательно. Стремление излагать материал просто и доступно даже для начинающего читателя-исследователя определило и элементарность используемых понятий, определений и средств. Это, конечно же, не означает, что все в текстах очень просто. Для усвоения содержания и смысла любой работы от читателя всегда требуются определенные усилия и временные затраты. Предлагаемые вниманию читателя работы не являются легким чтивом, это не перечисление любопытных занимательных фактов. Поверхностное ознакомление с работами у некоторых читателей оставляет вообще ощущение лженауки или чуши. Что с этим можно поделать? Даже советовать не хочу.
Личный опыт показывает, насколько трудно бывает вникнуть в чужую работу, если ее автор не ставил перед собой задачу сделать ее для читателя доступной и понятной, не сопроводил сквозным числовым примером и еще злоупотребляет словосочетанием «отсюда легко следует…». Даже П. Лапласу однажды пришлось на одно такое «отсюда легко следует…» потратить около двух месяцев для восполнения пробела.
Для себя считаю, что хорошим примером изложения порой не простых вопросов являются оригинальные тексты Эйлера или Ньютона. Сейчас в таком стиле не пишут. Рекомендую, если повезет, у букиниста откройте старый фолиант этих авторов и полистайте его. Латынь, на которой написан текст, можно пропустить, но математические выкладки вполне современны и вызывают восхищение. Подробно, неторопливо выполняются даже простые преобразования, и, видимо, также комментируются формулы латинским текстом.

Проблема факторизации напрямую связана с определением криптостойкости RSA, которое базируется на предположении, что не существует быстрых алгоритмов факторизации, которые за короткое время позволили бы взломать код, а если через некоторое время и получится это сделать, то данные потеряют свою актуальность. В этой статье мы протестируем и сделаем выводы по одному из способов факторизации.

Приведём определение факторизации.

Факторизацией целого числа называется его разложение в произведение простых сомножителей. Такое разложение, согласно основной теореме арифметики, всегда существует и является единственным (с точностью порядка следования множителей).

Будем обозначать число, которое требуется разложить буквой N, а два сомножителя, в результате умножения которых получим N, как a и b.

Алгоритм факторизации Ленстры (факторизация на эллиптических кривых) является одним из самых быстрых методов факторизации. Он имеет много общего с методом Полларда (p – 1), но работает значительно быстрей, следует отметить, что он является субэкспоненциальным методом. Главная особенность алгоритма – это то, что время, затраченное на факторизацию, зависит не от размерности N, а от размера наименьшего делителя числа N.

Подробно про этот метод вы сможете почитать из материала в списке использованной литературы, но всё же приведём основные стадии алгоритма.

1. Введём число N.
2. Выберем некоторое значение B, которое является максимальным пределом числа-делителя N.
3. Сгенерируем случайным образом значения x,y,a, которые принадлежат множеству целых чисел от 0 до N-1. Эти значения определяют кривую, а так же x и y определяют начальную точку P.
4. Вычислим b = y^2-x^3-ax mod n и g = Н.О.Д.(N, 4a^3+27b^2). Важно, что бы g не был равен N, иначе возвращаемся к п.2. Если 1 Теги:
5. факторизация
6. эллиптические кривые
7. Алгоритм Ленстры

Добавить метки

В настоящее время самыми эффективными алгоритмами факторизации являются вариации решета числового поля:

• Специальный метод решета числового поля со сложностью (метод применим для факторизации чисел только специального вида);
• Общий метод решета числового поля со сложностью (метод применим ко всем числам).

Применение в криптографии

Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA.

Ссылки

• Варновский Н. П. Проблема P =? NP, классы сложностей и криптография, 2005.
• Д. Кнут Раздел 4.5.4. Разложение на простые множители // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М .: Вильямс, 2007. — Т. 2. Получисленные алгоритмы. — С. 425—468. — 832 с. — ISBN 0-201-89684-2
• Ю. И. Манин, А. А. Панчишкин. I.2.3. Разложение больших чисел на множители // Введение в теорию чисел. — М .: ВИНИТИ, 1990. — Т. 49. — С. 72—106. — 341 с. — (Итоги науки и техники. Серия «Современные проблемы математики. Фундаментальные направления».).
• Ю. В. Нестеренко.Глава 4.7. Как раскладывают составные числа на множители // Введение в криптографию / Под ред. В. В. Ященко. — Питер, 2001. — 288 с. — ISBN 5-318-00443-1

Wikimedia Foundation . 2010 .

Смотреть что такое "Факторизация целых чисел" в других словарях:

Рекорды факторизации целых чисел — Факторизация простого числа это процесс определения простых чисел, являющихся делителями данного числа. Числа общего вида Первой очень большой распределенной факторизацией была факторизация RSA 129. Это число было разложено между сентябрем 1993… … Википедия

Факторизация — Эта статья о математической концепции. Другие значения термина в заглавии статьи см. на Фактор. Иллюстрация полинома x2 +&#1 … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Метод квадратичных форм Шенкса — метод факторизации целых чисел, основанный на применении квадратичных форм, разработанный Даниелем Шенксом (англ. Daniel Shanks).[1] в 1975 году, как развитие метода факторизации Ферма. Для 32 разрядных компьютерах алгоритмы, основанные на… … Википедия

Простое число — Простое число это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы… … Википедия

Алгоритм Блюма — Алгоритм Блюм Блюма Шуба (англ. Algorithm Blum Blum Shub, BBS) это генератор псевдослучайных чисел, предложенный в 1986 году Ленор Блюм, Мануэлем Блюмом и Майклом Шубом (Blum et al, 1986). BBS выглядит так: где является… … Википедия

Алгоритм Блюма — Блюма — Шуба — Алгоритм Блюма Блюма Шуба (англ. Algorithm Blum Blum Shub, BBS) это генератор псевдослучайных чисел, предложенный в 1986 году Ленор Блюм, Мануэлем Блюмом и Майклом Шубом (Blum et al, 1986). BBS выглядит так: где M = pq является… … Википедия

Блюм-Блюм-Шуб — Алгоритм Блюма Блюма Шуба (англ. Algorithm Blum Blum Shub, BBS) это генератор псевдослучайных чисел, предложенный в 1986 году Ленор Блюм, Мануэлем Блюмом и Майклом Шубом (Blum et al, 1986). BBS выглядит так: где M = pq является произведением… … Википедия

Нерешённые проблемы информатики — В этой статье приводится список нерешённых проблем информатики. В информатике проблема считается нерешенной, если эксперт в этой области считает проблему нерешенной, либо если несколько экспертов расходятся во мнениях по поводу её решения.… … Википедия

IEEE P1363 — IEEE P1363 проект Института инженеров по электротехнике и электронике (англ. Institute of Electrical and Electronics Engineers, IEEE) по стандартизации криптосистем с открытым ключом. Целью проекта было объединение опыта разработчиков… … Википедия