Как нарисовать четырехугольную призму
Содержание
- Определение призмы
- Виды призм
- Объем и площадь призмы
- Что такое призма
- Высота призмы
- Прямая призма
- Правильная призма
- Главная формула объема призмы
- Необычная формула объёма призмы
- Объем правильной треугольной призмы
- Объем правильной четырёхугольной призмы
- Объем правильной шестиугольной призмы
- Площадь поверхности призмы
- ПРИЗМА. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
- Теперь я хочу услышать тебя!
- P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂
- Комментарии
- Рисуем четырехгранную призму
- Шестигранная призма
- Зачем уметь строить эту геометрическую фигуру?
- Элементы правильной четырехугольной призмы
- Свойства правильной четырехугольной призмы
- Формулы для правильной четырехугольной призмы
- Указания к решению задач
- Задача.
- Задача
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Сейчас я расскажу тебе ВСЕ о призме. Без воды. Только то, что нужно.
Помни о своей цели! Тебе нужно подготовиться к ЕГЭ по математике так чтобы поступить в ВУЗ мечты!
Это самый лучший материал в инете.
Посмотри отзывы внизу статьи и ты все поймешь. И, кстати, можешь оставить свои.
Ладно, хватит болтать — к делу!
Определение призмы
 |
|
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
Виды призм
 |
|
 |
|
 |
|
Объем и площадь призмы
Главная формула объема призмы:
где — площадь основания,
Необычная формула объема призмы:
где — площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра.
Площадь полной поверхности призмы – сумма площадей всех граней.
А теперь подробнее.
Что такое призма
Давай ответим сперва картинками:

Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями. Остальные грани называются боковыми.
Плоскости оснований параллельный. Боковые грани – параллелограммы.

Смотри: бывают рёбра основания и боковые рёбра.

Важно знать, что:
| Все боковые рёбра призмы равны и параллельны. |
- Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то – четырёхугольной и так далее.
- Бывают и десятиугольные, и двадцатиугольные призмы, но , к счастью, не в твоих задачах.
- А у тебя будут встречаться чаще всего треугольные, четырёхугольные и шестиугольные призмы.
Высота призмы
| Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания. |

И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.
Прямая призма
Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
 |
У прямой призмы:
- все боковые грани прямоугольники;
- все сечения проходящие через боковые рёбра – прямоугольники;
- и даже сечения, проходящие только через одно боковое ребро — прямоугольники.
У прямой призмы высота совпадает с боковым ребром.
Правильная призма
Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.
То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Тебе, скорее всего, может встретиться:
1) Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.

2) Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.

3) Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

Главная формула объема призмы

Эта формула верна для любой призмы, но если призма прямая, то «превращается» в боковое ребро. И тогда
– то же самое, что

Необычная формула объёма призмы
Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы .
— площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра.

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.
Давай теперь для упражнения посчитаем объём самых популярных призм.
Объем правильной треугольной призмы
Пусть дано, что сторона основания равна , а боковое ребро равно .

Вспомним, как находить площадь правильного треугольника

Подставляем в формулу объёма:
Объем правильной четырёхугольной призмы
Опять дано: сторона основания равна , боковое ребро равно .

Ну, площадь квадрата долго искать не надо:
Объем правильной шестиугольной призмы

Что же такое ? Как найти?
Смотри: шестиугольник состоит из шести одинаковых правильных треугольников.

Площадь поверхности призмы
| Площадь боковой поверхности призмы – сумма площадей всех боковых граней. |
Есть ли общая формула?
Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.

Площадь полной поверхности призмы – сумма площадей всех граней.

Формулу можно написать для прямой призмы:
Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.
, где — периметр основания.

Для примера посчитаем полную поверхность правильной шестиугольной призмы.
Пусть сторона основания равна , а боковое ребро равно .

Все боковые грани – прямоугольники. Значит .
— это уже выводили при подсчёте объёма.
ПРИЗМА. КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
 |
|
Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.
 |
|
 |
|
 |
|
3. Объем и площадь призмы:
- Главная формула объема призмы :
,
где — площадь основания,
— высота. - Необычная формула объема призмы:
,
где — площадь сечения, перпендикулярного боковому ребру,
— длина бокового ребра. - Площадь полной поверхности призмы – сумма площадей всех граней.
.
Теперь я хочу услышать тебя!
Я постаралась сжато, без воды рассказать о том, что такое призма.
Что тебе понравилось? Что не понравилось?
Может быть ты нашел ошибку?
Или знаешь другой хороший материал на эту тему?
Напиши внизу, в комментариях.
P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это — не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте — нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Я рекомендую использовать для этих целей наш учебник "YouClever" (который ты сейчас читаешь) и решебник и программу подготовки "100gia".
Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!
И в заключение.
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” — это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Комментарии
Огромное вам спасибо за созданный сайт,он очень удобен и информативен.Мне сложно представить какое количество времени было потрачено на "переработку" материала в понятном и доступном виде.Теперь есть источник чистых знаний,без лишней "воды",который не только помогает узнать новое,но и систематизировать информацию в голове .Жаль,что я не нашел сайт раньше.Вы лучшие!
Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке
Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.
В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.
Рисуем четырехгранную призму
Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.
Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).
Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.
Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.
Шестигранная призма
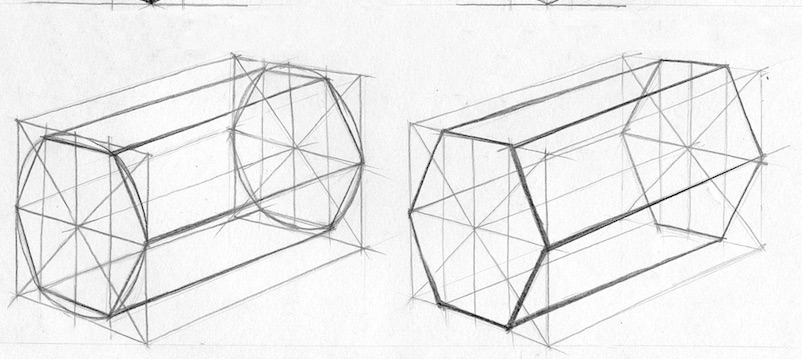
Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.
Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.
Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.
Зачем уметь строить эту геометрическую фигуру?
Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.
С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.
Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.
Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.
В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.
Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.
Элементы правильной четырехугольной призмы

- Основания ABCD и A1B1C1D1 равны и параллельны друг другу
- Боковые грани AA1D1D, AA1B1B, BB1C1C и CC1D1D, каждая из которых является прямоугольником
- Боковая поверхность — сумма площадей всех боковых граней призмы
- Полная поверхность — сумма площадей всех оснований и боковых граней (сумма площади боковой поверхности и оснований)
- Боковые ребра AA1, BB1, CC1 и DD1.
- Диагональ B1D
- Диагональ основания BD
- Диагональное сечение BB1D1D
- Перпендикулярное сечение A2B2C2D2 .
Свойства правильной четырехугольной призмы
- Основаниями являются два равных квадрата
- Основания параллельны друг другу
- Боковыми гранями являются прямоугольники
- Боковые грани равны между собой
- Боковые грани перпендикулярны основаниям
- Боковые ребра параллельны между собой и равны
- Перпендикулярное сечение перпендикулярно всем боковым ребрам и параллельно основаниям
- Углы перпендикулярного сечения — прямые
- Диагональное сечение правильной четырехугольной призмы представляет собой прямоугольник
- Перпендикулярное (ортогональное сечение) параллельно основаниям
Формулы для правильной четырехугольной призмы

Указания к решению задач
При решении задач на тему "правильная четырехугольная призма" подразумевается, что:
Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)
Задача.
В правильной четырёхугольной призме площадь основания 144 см 2 , а высота 14 см. Найти диагональ призмы и площадь полной поверхности.
Решение.
Правильный четырехугольник — это квадрат.
Соответственно, сторона основания будет равна √ 144 = 12 см.
Откуда диагональ основания правильной прямоугольной призмы будет равна
√( 12 2 + 12 2 ) = √288 = 12√2
Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 ) 2 + 14 2 ) = 22 см
Задача
Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.
Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:
a 2 + a 2 = 5 2
2a 2 = 25
a = √12,5
Высота боковой грани (обозначим как h) тогда будет равна:
h 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5
Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания
S = 2a 2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см 2 .

