Как выразить степень экспоненты
Содержание
- Определение
- Число e
- График экспоненты
- Формулы
- Частные значения
- Свойства экспоненты
- Область определения, множество значений
- Экстремумы, возрастание, убывание
- Обратная функция
- Производная экспоненты
- Интеграл
- Комплексные числа
- Выражения через гиперболические функции
- Выражения через тригонометрические функции
- Разложение в степенной ряд
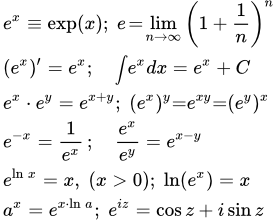
Определение
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e . Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045.
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
График экспоненты
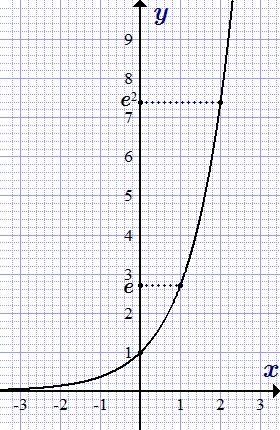
На графике представлена экспонента, е в степени х.
y ( x ) = е х
На графике видно, что экспонента монотонно возрастает.
Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е .
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
Частные значения
Пусть y ( x ) = e x . Тогда
.
Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1 .
Область определения, множество значений
Экспонента y ( x ) = e x определена для всех x .
Ее область определения:
– ∞ .
Ее множество значений:
0 .
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ |
| Область значений | |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
Обратная функция
Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Интеграл
Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Выражения через гиперболические функции
Выражения через тригонометрические функции
Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 25-02-2014 Изменено: 09-06-2018
Число е является важной математической константой, которая является основой натурального логарифма. Число е примерно равно 2,71828 с пределом (1 + 1/n) n при n , стремящемся к бесконечности.
Также данное число называют как число Эйлера или число Непера.
Экспонента — показательная функция f(x) = exp (x) = e x , где е — число Эйлера.
Введите значение х, чтобы найти значение экспоненциальной функции e x
Расчет значения экспоненциальной функции онлайн.
При возведении числа Эйлера (е) в нулевую степень ответ будет равняться 1. При возведении в степень, которая будет больше единицы, ответ будет больше первоначального. Если степень будет больше нуля, но меньше 1 (например, 0,5), то ответ будет больше 1, но меньше первоначального (числа е). При возведении экспоненты в отрицательную степень нужно 1 делить на число е в заданной степени, но со знаком плюс.
Теорию функций e z , sin z, cos z комплексного аргумента построил Л.Эйлер и систематически изложил ее в своем классическом труде «Введение в анализ бесконечно малых» в 1748 г. В следующем году он опубликовал теорию логарифма комплексного аргумента.
1. Начнем с показательной функции, которую Эйлер определил как сумму степенного ряда

Ряд сходится, причем абсолютно, при любом zeC. Действительно, составьте ряд из модулей членов ряда (6.1) и примените к нему признак Далам- бера. Такое определение показательной функции комплексного переменного положило начало анализа в комплексной области — ТФКП.
В литературе можно найти определение функции (6.1) тем же предельным соотношением, что и в действительном анализе:

но здесь исключительно используется представление (6.1). Важно, что для комплексных значений аргумента остается верной теорема сложения:
Проверим это свойство. Имеем

Раскроем скобки и будем располагать слагаемые по группам, в которых сумма показателей степеней при а и b одна и та же. Получим


При чисто мнимом z — yi согласно (6.1) имеем  Или, отделяя вещественную часть от мнимой,
Или, отделяя вещественную часть от мнимой,

Суммы рядов в скобках равны соответственно cos^,sin>>, и мы приходим к замечательной формуле Эйлера

Заметим, что этой формулой, в которой левая часть называлась символом Эйлера, мы неоднократно пользовались с целью компактификации вычислений с комплексными числами. До сих пор символ е ул употреблялся для сокращенного обозначения правой части формулы, а теперь можем его понимать как мнимую степень числа е. Например, равенство е я = -1 всегда вызывало восторг у математиков — ведь вроде бы несложной зависимостью оно увязывает между собой две знаменитые константы.
Из теоремы сложения при z = х + yi получим е : = е х • е у> , или

Заметим, что в учебной литературе это равенство часто берется за определение показательной функции комплексного переменного. Оно очень удобное, с его помощью можно, например, доказать голоморфность экспоненты во всей комплексной плоскости. В самом деле, полагая е г = t/ + /v, из (6.2) находим, что и = е х cosy,v = е х sin у. Эти функции везде дифференцируемы в смысле действительного анализа и для них выполняются условия Коши-Римана:

Сохраняется формула дифференцирования, знакомая из действительного анализа. Воспользуемся одной из записей комплексной производной:

При действительных значениях аргумента показательная функция положительная и, следовательно, в ноль не обращается. Из (6.2) заключаем, что е : ф 0 Vz е С (ведь не могут косинус и синус одновременно обратиться в ноль).
Из теоремы сложения и формулы Эйлера вытекает периодичность экспоненты с мнимым основным периодом 2 я7. Действительно,
е г * 2я> =е : ? е 2т =е : 1 = е ; , т.е. число 2я7 является периодом. Проверим, что он основной: ему кратен любой другой период Т. Пусть е г+ =е : . Умножая обе части на е
: , получим е г =. Полагая T = Ty+iT2, получим е 7| (cosТ2 +/sin Т2) = 1. Отсюда е 7 ‘ cosТ2 = 1, sin Т2= 0 согласно равенству двух комплексных чисел. Из полученных соотношений следует

2. Тригонометрические функции комплексного переменного. Следуя Эйлеру, положим

Нетрудно проверить, что эти ряды сходятся во всей комплексной плоскости.
Запишем равенство (6.1), заменяя в нем z на iz. Под ним выпишем (6.1) с заменой z на -iz. Складывая и вычитая полученные равенства, придем к соотношениям е ,: +е
а = 2cos z, е а -е

Эти формулы целиком сводят изучение тригонометрического синуса и косинуса к изучению показательной функции. Например, дифференцируя почленно вторую из них, придем к известному из анализа правилу дифференцирования (sin z)’ = cosz.
Основное тригонометрическое тождество оказывается справедливым. Возведите в квадраты обе части в (6.4) и затем сложите их; увидите единицу.
В комплексной области сохраняются теоремы сложения, знакомые еще со школы. Например, sin(a + 6) = sintf-cos6 + cosa*sin&. Для доказательства достаточно проверить, что

Выполнив операции, указанные в правой части, придем к рассматриваемой теореме сложения.
Обратим внимание на то, что синус и косинус в комплексной плоскости не являются ограниченными функциями. Например, положим z = it (/ > 0), тогда

что вовсе не согласуется с ограниченностью.
Как известно, в действительной области нули синуса исчерпываются числами, кратными /г, а нули косинуса содержатся в формуле
г = — + кл (к gZ). Возникает вопрос: нс появятся ли у этих функций, кроме
указанных, еще другие, комплексные нули при выходе на комплексную плоскость? Ниже мы увидим, других нулей нет.
Подводя итоги, мы видим, что рассмотренные выше функции можно определить и для комплексного аргумента и что известные из школьного курса формулы остаются справедливыми. Но обнаружился новый факт: показательная функция периодическая, хотя период мнимый. Такая периодичность в школьном курсе и нс могла быть обнаружена, так как в нем изучались только функции действительного аргумента.
3. Гиперболические функции комплексного переменного. В духе равенств (6.3) положим

Это — соответственно косинус гиперболический и синус гиперболический комплексного числа z. Ряды (6.5) сходятся, как и выше, при любых значениях Z.
Заменим в (6.1) z на —z и к исходному равенству прибавим полученное. По аналогии с (6.4) получим следующие выражения рассматриваемых функций через экспоненту:

При действительных z- х эти равенства чаще всего и берутся в качестве определений. Соответствующие графики представлены на рис. 12.


Из равенств (6.6) и устанавливаются основные свойства гиперболических функций. Исторически они были известны и до Эйлера. Возникая из ряда задач математической физики, обыкновенных дифференциальных уравнений, они широко использовались в приложениях, например, в электротехни- В литературе встречаются обозначения этих функций, когда аргумент заключается в скобки.
ке, сопротивлении материалов и т.д. Важную роль эти функции играют в геометрии Лобачевского.
Формулы (6.4) и (6.6) позволяют установить связи между тригонометрическими и гиперболическими функциями:

При мер. Вычислить приближенно с 4D sin(l -2/).
Решение. Искомое выражение равно sin 1 cos2/-cosl sin2/. Или, в свете предыдущих равенств, получим sin 1 c/?2-/cosl shl. Ответ: 3.1659-1.9595/.
Пример. Доказать, что нули функции sinz исчерпываются формулой z — 7Гк (k^Z).
Решение. Пусть sin z = sin(.v + yi) = 0 sin * • cosyi + cos*• sinyi = 0. Ho здесь cosyi=chyy sin yi = ishy, поэтому sin x • chy+/cos* • shy = 0. Отсюда заключаем, что sin*c/?y = 0, cos*-shy = 0. Так как гиперболический косинус при действительном значении аргумента в нуль не обращается (рис. 12), то sin* = 0=>* = як <к eZ).Тогда из второго уравнения
cosxk s/jy = 0 =>shy = 0 у = 0. Итак, все корни уравнения sinz = 0 заключаются в формуле z = x + iy = 7rk. К такому же результату привела бы вторая формула в (6.4). Советуем читателю проделать более краткие выкладки.
4. Логарифмы и общая степенная функция.
В области действительных чисел ноль и отрицательные числа логарифмов не имеют. Выясним, как обстоит дело при переходе в область комплексных чисел. Определим понятие натурального логарифма комплексного числа так же, как в действительном анализе.
Число w называется натуральным логарифмом данного комплексного числа z, если е" = z.
Исторически первая удовлетворительная теория логарифма была дана Л.Эйлером в 1749 г., который исходил из следующего определения:

Поскольку показательная функция нс принимает нулевого значения, то ноль не имеет логарифмов в комплексной области. В силу периодичности экспоненты у числа z логарифм не единственный. Например, для z = l в качестве логарифмов можно взять числа -w—2nki (keZ). Множество всех натуральных логарифмов данного числа z^O обозначается символом Lnz.
В равенстве e w = z положим w=u + iv. Обозначим через г модуль данного комплексного числа z^O, через (р — его главное значение аргумента. Получим

Так как модули левой и правой частей одинаковы, то отсюда е и =/* и = In г. Здесь под правой частью последнего равенства следует понимать обычный натуральный логарифм положительного числа г. Далее из равенства (*) заключаем, что аргументы чисел справа и слева могут отличаться друг от друга только на кратное 2л: v = (р + 2кл (к eZ). Поэтому множество всех логарифмов описывается формулой

Значение логарифма, равное In | z|+/argz, называют главным значением логарифма и обозначают символом In z. Поэтому вес значения Lnz получаются из главного добавлением кратных 2лi.
Пример, а). Найти Lnz при r = l + i. б). Чему равен Ln(-1) ?
Решение, а). Имеем: | z I = Jl, argz = —. Ответ: In л/2 н—/’ + +2&я/.
Для чисел w,zeC <0>по правилам «в действительной области логарифм произведения равен сумме логарифмов», «в комплексном анализе аргумент произведения равен сумме аргументов» запишем следующие равенства:

Получается, что первое правило распространяется и на комплексную область: Ln(wz) = Lnw+ Lnz. Это равенство надо понимать в следующем смысле: множество, составленное из всевозможных сумм двух слагаемых, одно из которых принадлежит Lnw, а другое Lnz, совпадает с множеством значений Ln(wz).
Итак, мы видим, что логарифмы можно находить не только положительных чисел, как это делается в школе, но и для комплексных чисел. Обнаруживается, что логарифмическая функция (6.7) не однозначная, как это имеет место в действительном анализе, а многозначная: каждое комплексное число, отличное от нуля, имеет бесконечное множество логарифмов. В частности, имеют логарифмы и отрицательные числа, но при этом все они комплексные. Положительные же числа, кроме действительного значения логарифма, рассматриваемого в школьном курсе, имеет еще счетное множество комплексных логарифмов.
Обратимся к дифференцированию комплексного логарифма. Ясно, что достаточно уметь находить производную главного значения (ибо производные от констант — нули). Дифференцируя (по z ) равенство е и = z, получим
е* -м/ = 1 => w = —. Пришли к знакомой формуле из действительного анализа

Заметим, что эта формула верна всюду, где главное значение логарифма непрерывно. Разрывы происходят лишь в точках отрицательной действительной полуоси, ибо в них, как мы видели ранее, разрывно главное значение аргумента вследствие определения его на оговоренном промежутке (-тг,тг].
В действительном анализе имеет место равенство а ь =е Ша . В комплексном анализе пользуются аналогичной формулой, но она выполняет уже роль определения а ь . А именно, полагают
 I
I
Так, при ненулевых а,Ь определена степень с произвольным показателем. Так как логарифм имеет бесконечное множество значений, то и выражение а ь в общем случае — также, но в частных случаях они могут все совпадать (если b — целое число) или среди них может быть только конечное число различных значений (если степень b является рациональным числом).
Рассмотрим, например, V. Согласно (6.8) получим е =е 2 , где п
— целое число. Неискушенному этот пример покажется очень удивительным: мнимое число возводится в мнимую степень и получается бесконечно много значений, да еще все они — действительные числа!
Другой пример: найти согласно (6.8) величину / 3 . Ответ

согласуется с перемножением мнимой единицы самой на себя три раза.
J 1 ж. « „ • v, 1, „ 2кт
Вычислим w=8 3 . Имеем: w = e 3 =е 3 •е 3 . Здесь первый
множитель равен 2, а второй принимает лишь три различные значения (например, при к = 0,1,2. Далее начнется повтор).
5. Аркфункции и ареафункции комплексного аргумента.
Аркфункцня (от лат. arcus — дуга) — то же, что обратная тригонометрическая функция, т.е. одна из функций: арксинус, арккосинус, арктангенс, . ; соответствующие обозначения Arc sin z, Arccosz, Arctgz, .
Ареафункция (от лат. area — площадь) — то же, что обратная гиперболическая функция, т.е. одна из функций: ареасинус гиперболический (Arshz)y ареакосинус гиперболический (Arch-), аретангенс гиперболический (Arthz) и т.д.
Эти обозначения, как и предыдущие, не являются общепринятыми, возможны и другие написания рассматриваемых функций. Они, будучи обратными к многолистным функциям (синус, косинус, . ), являются многозначными и выражаются через корни и логарифмы. Найдем такое выражение, например, для арккосинуса — решим при заданном z уравнение cosw=z.
Или, что то же, уравнение — (е ,и +е — ‘") = z как квадратное относительно e ,w .

(мы нс пишем здесь перед корнем обычный знак ± f ибо в комплексном анализе квадратный корень и так имеет два значения). Из последнего равенства получим


Подобным же способом получаются выражения для ареафункций:

Укажем еще группу формул, выражающих ареафункции через арк- функции:

В заключение рассмотрим следующий пример.
При мер. Решить уравнение sinw=2.
Решение. Согласно (6.9) имеем w= Arcsin2 = -iLn <2i + у1 1 -2 2 ). Здесь радикал принимает два значения ± л/З /. Находим логарифм. Так как числа 2 ± -Уз оба положительные, то он равен

Следовательно, w = — + 2лк + i 1п(2 + v’3 , так как (2 ± л/З) ‘=2 + л/3. Читателю рекомендуем сделать проверку. Использовать теорему сложения в виде

и равенство cos iz = chz.
Задачи к главе 6
6.1. Доказать, что число п является основным периодом функции sinz
6.2. Докажите теорему сложения для гиперболического косинуса:

Каков аналог теоремы для гиперболического синуса?
- 6.3. Верна ли формула ln( zw) = In z + In w ? А формула Ln(z 2 ) = 2Lnz ?
- 6.4. Доказать, что при возведении комплексного числа а* 0 в иррациональную степень а получается бесконечно много значений и все они лежат на окружности с уравнением | z |=| а а .
- 6.5. Решить уравнение cosz = 8.

