Как построить линию пересечения плоскостей начертательная геометрия

Построение линии пересечения двух плоскостей.

Одной из основополагающих задач начертательной геометрии является задача на на построение линии пересечения двух плоскостей общего положения. Случаи задания плоскостей бывают разные, но в любом случае вам встретится задача, в которой будет необходимо построить линию пересечения двух плоскостей заданных треугольниками (или другими плоскими геометрическими фигурами). Алгоритм решения такой задачи я и предлагаю рассмотреть сейчас.

(Если же ваши плоскости заданы не треугольниками, а, например, параллельными прямыми, то приглашаю вас прочитать еще один урок, посвященный тому, как найти линию пересечения двух плоскостей.)

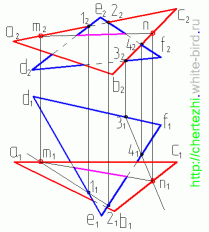
Итак, даны две плоскости, заданные треугольниками АВС и DEF. Метод сводится к тому, что бы поочередно найти две точки пересечения двух ребер одного треугольника с плоскостью другого. Соединив эти точки мы получим линию пересечения двух плоскостей. Построение точки пересечения прямой с плоскостью более подробно было рассмотрено в предыдущем уроке, напомню только механические действия:

— Заключим прямую АС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми DE и DF — точки 1 и 2
— На горизонтальной проекции соединим проекции точек 1 и 2 и найдем точку пересечения получившейся линии с горизонтальной проекцией той прямой, которую мы заключали во фронтально-проецирующую плоскость, в этом случае — с прямой AC. Мы получили точку M.
— Заключим прямую BС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми EF и DF — точки 3 и 4
Соединим их горизонтальные проекции и получим точку пересечения этой прямой с прямой ВС — точку N.
— Соединив точки M и N мы получим линию пересечения плоскостей заданных треугольниками. По сути линия пересечения уже найдена. — Осталось лишь определить видимость ребер треугольников. Это делается методом конкурирующих точек.

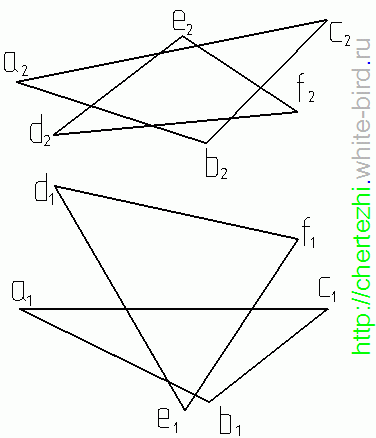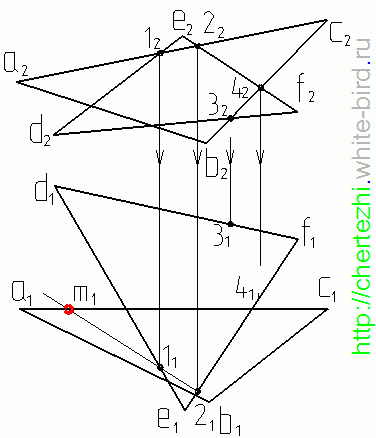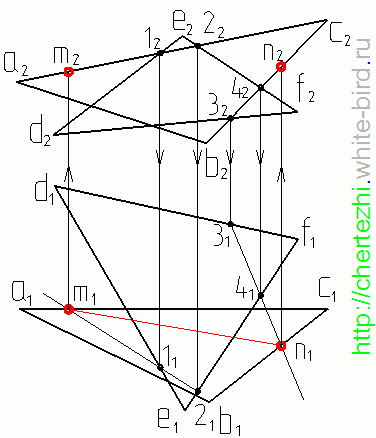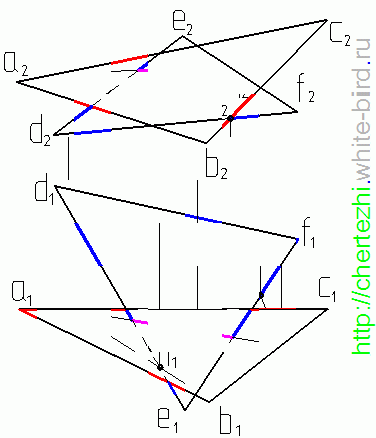
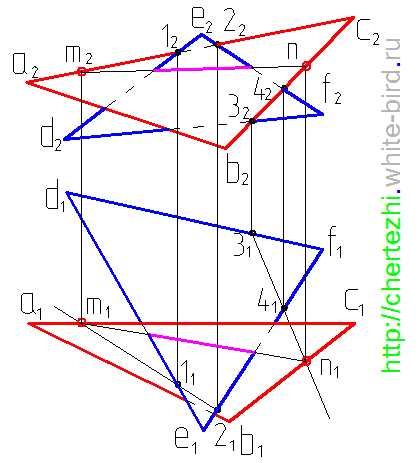
При помощи наиболее внимательных посетителей сайта удалось найти неточность при определении видимости плоскостей. Ниже приведен чертеж, на котором исправлена видимость линий, ограничивающих плоскости на горизонтальной плоскости проекций:

Вы можете сказать "спасибо!" автору статьи:

пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам"

или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи

или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.

А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны:

Автор комментария: Сир_Иван
Дата: 2010-12-19

а я понять не мог никак, спасибо.

Автор комментария: надежда
Дата: 2011-12-13

Автор комментария: Дебердеева
Дата: 2012-01-20

Ну, тут как говорится, Кесарю — кесарево 🙂

Автор комментария: макс
Дата: 2012-01-23

Автор комментария: Леха
Дата: 2012-03-20

Автор комментария: степан
Дата: 2012-03-30

Автор комментария: Хадыжа
Дата: 2012-03-31

Исключительно , замечательно. Доходчиво и просто. Спасибо большое

Автор комментария: Саня
Дата: 2012-10-02

Большое спасибо, очень доходчиво написано!

Автор комментария: Алька
Дата: 2012-10-07

Автор комментария: инна
Дата: 2012-10-12

ААААААААААААААААААААААААА. вы спасли меня.

Автор комментария: Степан
Дата: 2012-10-13

Автор комментария: Сан
Дата: 2012-10-17

подскажите пожалуйста. Можно ли строить все тоже самое , но из вида сверху, на вид спереди. т.е из нижних 2х треугольников на верхнии? По такому же алгоритму

Автор комментария: Владислав
Дата: 2012-11-05

Вот спасибо, товарищи!)) Отличная статья!

Автор комментария: Всеволод
Дата: 2012-11-07

Хух спасибо выручили и руп в ближайшее время кину

Автор комментария: Дмитрий
Дата: 2012-11-10

Неправильно определена видимость треугольников в плоскости XY. Легко проверить методом конкурирующих точек. [URL=http://www.radikal.ru][IMG]http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg[/IMG][/URL]

Автор комментария: Дмитрий
Дата: 2012-11-10

Хотел вставить картинку с пояснениями, а тут тег [IMG] [/IMG] не работает. Пояснения здесь http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg

Автор комментария: Александр
Дата: 2012-11-12

To Дмитрий: Согласен, что ошибка в видимости, но только не в XY, а в XZ. Сделал подобный чертез в простеньком 3D редакторе: http://s59.radikal.ru/i163/1211/8b/bc5f07b225d9.jpg Так должно быть. =)

Автор комментария: Александр
Дата: 2012-11-12

Да и если просто логически подумать, то понятно, что линия df (которая на XY виде выше всех) никак не может на виде сверху (XZ) быть под красным треугольником.
Александр, Дмитрий, спасибо за внимательность, исправлю на днях! Как говаривал наш преподаватель по вышке, уже весьма давно: "Молодчики! Бдительность — наше единственное оружие!"

Автор комментария: Дмитрий
Дата: 2012-11-12

Александр, возможно, я ошибся. Но давайте проверим видимость в плоскости XZ с помощью конкурирующих точек. В моем примере это G и H см. рис. http://s47.radikal.ru/i118/1211/b9/d29b24b27c65.jpg Кажется все правильно. Поправьте меня если это не так.

Автор комментария: Александр
Дата: 2012-11-12

Да, Дмитрий, сейчас немного подумал и понял, что просто перепутал фронтальный и горизонтальный виды, поэтому все с точьностью наоборот получилось. Вы правы. =)

Автор комментария: Черт
Дата: 2012-11-14

Бред.
Да, согласен. Бред. Так говорят все, это нормально. См. рубрику Юмор

Автор комментария: рома
Дата: 2012-12-07

спасибо большое! мне эта стаття очень помогла. очень доходчиво был показан алгоритм на анимации. спасибо, еще раз:)))

Автор комментария: Антон
Дата: 2012-12-08

А если у меня не получается одна из точек,т.е точка м не лежит на ас,что делать?
Антон, доброго дня. Если вы имеете ввиду, что линия проведенная через 12 проходит мимо АС- просто продлите отрезок АС таким образом, чтоб все же найти точку пересечения этих ПРЯМЫХ. Их отрезки- лишь обозначенная их часть. Так что смелее. Это часто встречается.

Автор комментария: Людмила
Дата: 2012-12-13

помогите сделать контрольную A — 0 55 40 B — 50 110 0 C — 120 40 75 D — 10 80 80 E — 80 20 90 F — 110 80 5 два треуг. ABC и DEF
Дорогие студенты. Если у вас ВДРУГ возникает желание написать подобное сообщение, не закапывайте свой шанс получить быстрый ответ. Пишите сразу на почту, с указанием сроков, телефона для связи и если нужно ОЧЕНЬ БЫСТРО — предлагайте стоимость и способ оплаты. Причем надо быть готовым к оплате вперед. А еще. иногда я бываю занят 🙂

Автор комментария: Арман
Дата: 2013-01-14

Автор комментария: Александр
Дата: 2013-01-24

Спасибо огромное! ГИФка просто супер, все понятно)

А ведь есть и те, кому не нравится 🙂 Но я не в силах отказаться от этого "спорта"! Жаль только, что никак не найду времени исправить ошибку.

Автор комментария: Варя
Дата: 2013-01-31

Огроменное Вам спасибо.

Автор комментария: Андрей
Дата: 2013-02-07

Автор комментария: игорь
Дата: 2013-04-18

мне нужно построить пересечение двух непрозрачных фигур треугольника ABC и параллелограмма DEFG. координаты а(185.140.115)b(0.30.45)c(105.0.15)d(165.115.0)e(215.55.30) f(65.25.115) вот вопрос почему один из треугольников не пересекается с параллелограммом и можно ли решить эту задачу!

Автор комментария: Юра
Дата: 2013-09-21

Автор комментария: Сергей
Дата: 2013-12-22

Автор комментария: бес
Дата: 2014-11-16

Автор комментария: Лера
Дата: 2015-10-17

Спасибо огромное! Мучаюсь уже около часа, методичка не помощник, а Ваша гифка все расставила на свои места!

Лера, вы молодец! А ведь что интересно: многие ругают мою псевдонимацию 🙂 Успехов вам!

Автор комментария: Иван
Дата: 2015-11-23

Полностью присоединяюсь к Лере) Ваша гафа просто четкая. Наглядно видно что да как делать. Все супер. Спасибо)

Автор комментария: гость
Дата: 2015-12-28

Автор комментария: Василий
Дата: 2016-10-13

Спасибо! Всё понятно. Чётко и без мути

Добавьте свой комментарий:

zakaz@triv >Наша страница в ВК:

Всем, кто будет в будущем решать, звонить сюда, или кому-то еще — однозначно говорю — сюда. Есть с чем сравнить. В прошлом году заказывал начертательную геометрию в другом месте — устал звонить чтоб отдали чертежи и методичку. Здесь же — отдали готовые чертежи день в день как изначально договорились. Чертежи чистые и препод даже не придрался, хотя меня и предупредили, что могут попросить что-то немного подправить. Еще раз спасибо, очень выручили.

Сергей, благодарю вас, что нашли время отписаться. Кстати о времени — нелегко было сделать ваши пять листов за один день. Старайтесь впредь так не затягивать! Обращайтесь, если еще будет нужно, хотя черчение у вас уже закончилось..

Две плоскости всегда пересекаются по прямой. Для построения линии пересечения достаточно найти две точки этой линии или одну точку и направление этой прямой. Рассмотрим несколько случаев пересечения плоскостей.

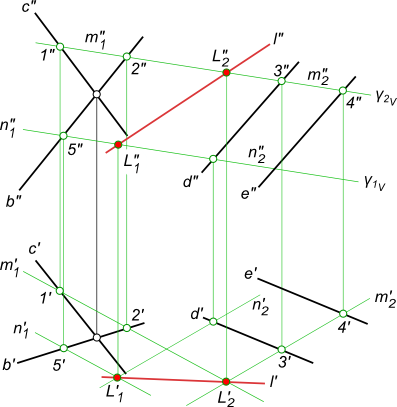
Пример 1. Две плоскости α и γ пересекаются по прямой MN (рис.60) в пределах чертежа.

(•) М (М₁, М") и (•) N (N₁, N") есть точки пересечения одноименных следов (рис.60).

Пример 2. Пересечение двух плоскостей происходит по горизонтали (или фронтали).

На рис.61, 62 фронтальная проекция лини пересечения совпадает со следом f_0γ, а горизонтальная легко находится как горизонтальная проекция горизонтали в этой плоскости.

Пример 3. В пределах чертежа пересекаются только два горизонтальных следа заданных плоскостей α и β(рис63).

Рис.63

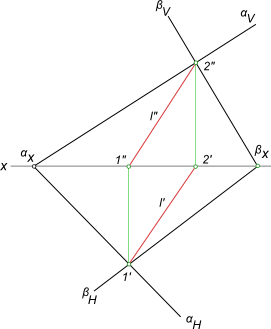
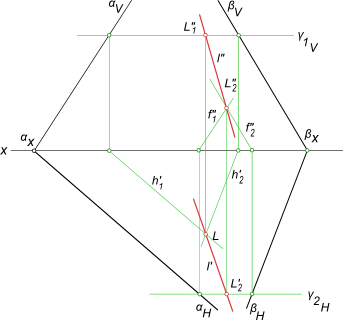
Точку М находим в пересечении горизонтальных следов. Для нахождения точки N возьмем дополнительную вспомогательную горизонтальную плоскость γ. Эта секущая плоскость будет пересекать плоскости α и β по горизонталям. Горизонтальные проекции этих горизонталей в пересечении дадут вторую точку линии пересечения плоскостей α и β — точку N (рис.64).

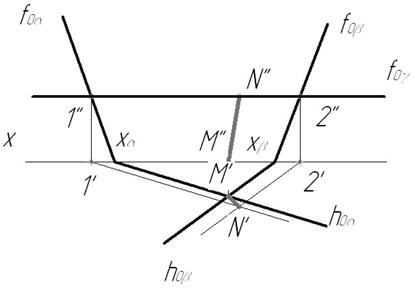Рис.64

Пример 4. Одна плоскость задана следами общего положения, вторая плоскость задана двумя пересекающимися прямыми общего положения (рис.65).

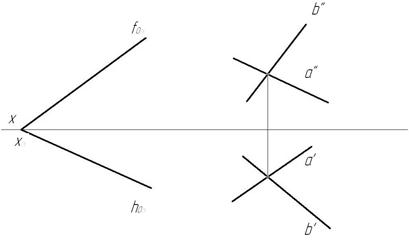Рис.65

1. Проведем вспомогательную плоскость частного положения, например, плоскость горизонтального уровня β ׀׀ π₁ (f_оβ ׀׀х) (рис. 66).

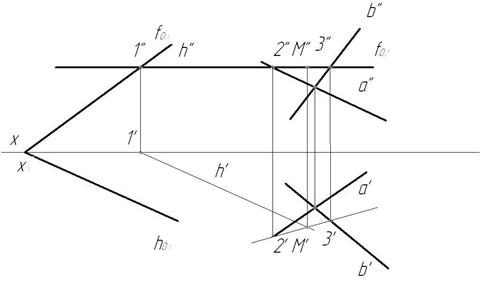Рис.66

2. Плоскость β пересечет плоскость α по горизонтали h. h» 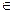f_оβ,h’׀׀h_оα..

3. Плоскость β пересечет плоскость (а∩b) по прямой (2-3).

4. Прямые h и 2-3 пересекаются в точке M (M’ и M»), где M’=h’∩(2′-3′), а M» 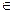f_оβ.

5. Для построения второй общей точки проведем еще одну вспомогательную плоскость γ ׀׀ π1 (fоγ׀׀ х) ( рис.67).

6. Плоскость γ пересечет плоскость α по горизонтали h1: h1» 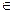f_оγ, h1′׀׀h_оα.

7. Плоскость γ пересечет плоскость (а∩b) по прямой (5-6).

8. Прямые h1 и 5-6 пересекутся в точке М (М» и М’), где М’=(5′-6′) ∩h1′, М» 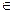f_оγ.

9. Соединим одноименные проекции точек М и N и получим проекции линии пересечения (М’N’) и (М»N»).

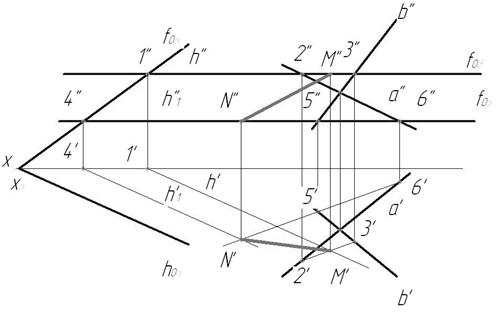Рис.67

Пример 5. Плоскость ΔАВС частного положения (ΔАВС 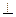π₁), плоскость ΔMNK – общего положения (рис.68).

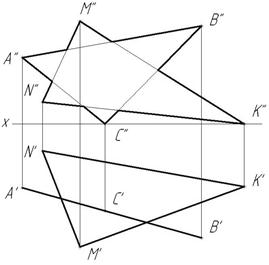Рис.68

Поскольку ΔАВС 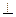π₁, горизонтальная проекция ΔА’В’С’ обладает собирающими свойствами, т.е. горизонтальная проекция линии пересечения лежит на горизонтальной проекции ΔА’В’С’.

1. Отметим общие горизонтальные проекции Q’ и T’ на пересечении горизонтальных проекций треугольников АВС и MNK (рис.69).

2. Фронтальные проекции Q» и T» ищем на линиях проекционной связи в ΔM»N»K».

3. Линия пересечения QT определена QT (Q»T» и Q’T’).

4. Определим видимость плоских фигур, т.к. плоскости считаются непрозрачными. Видимость горизонтальной проекции фигур определять не надо, т.к. ΔАВС проецируется в прямую линию, проекция M’N’K’ видима. Определим видимость плоских фигур относительно плоскости проекций π₂. Для этого рассмотрим конкурирующие точки 1 и 2, лежащие на скрещивающихся прямых ВС и МK. Фронтальные проекции 1" и 2" совпадают, а горизонтальная проекция 2′ находится перед горизонтальной проекцией 1′. Точка 1» невидима относительно плоскости проекций π₂. Далее рассуждаем так: точка 2 лежит на ΔАВС, следовательно, фронтальная проекция ΔА»В»С» видима на π₂ с той стороны, где находятся точки 1» и 2». После фронтальной проекции линии пересечения Q" и T" видимость ΔА»В»С» меняется на противоположную, т.е. он становится невидимым (рис.69).

Рис.69

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8833 — | 7547 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две точки, принадлежащие одновременно каждой из двух заданных плоскостей — так называемые общие точки.

Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ₁ и γ₂.

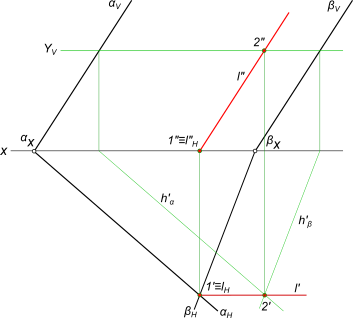
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и параллельными прямыми d e.

Вспомогательная плоскость γ₁ пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии. Вспомогательная плоскость γ₂ пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии. Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей — линию l.

Пересечение двух плоскостей, заданных треугольниками ABC и DEF.

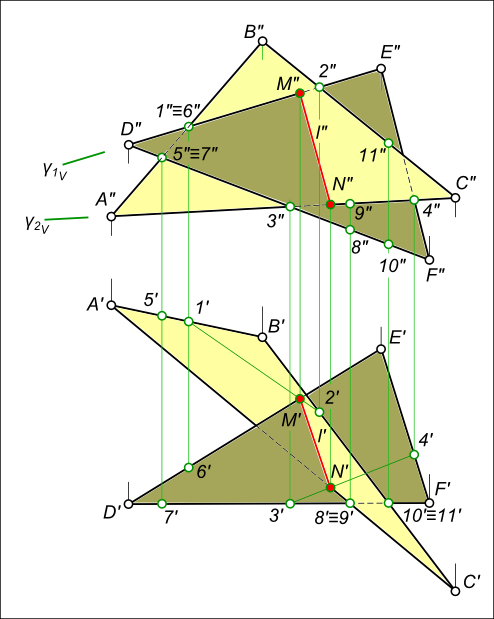
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии — точка M. Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии — точка N. Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.

Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки: на фронтальной плоскости проекций — 1"≡6"; 1`, 6` и 5"≡ 7"; 5`, 7` — будет видна вершина D с прилегающими сторонами до линии пересечения. на горизонтальной плоскости проекций — 8`≡9`; 8", 9" и 10`≡ 11`; 10", 11" — будет видна вершина C с прилегающими сторонами до линии пересечения.

Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)

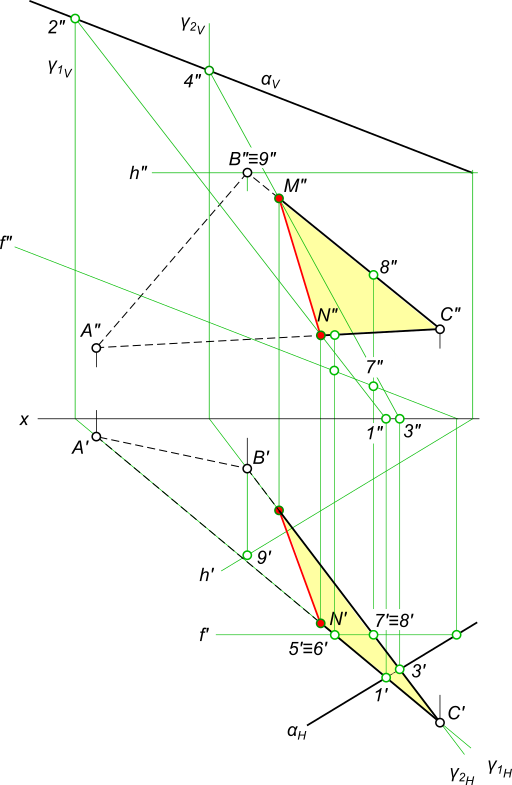
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом