Как посчитать натуральный логарифм в excel

Одним из востребованных математических действий при решении учебных и практических задач является нахождение логарифма из заданного числа по основанию. В Экселе для выполнения данной задачи существует специальная функция, которая называется LOG. Давайте поподробнее узнаем, как её можно применять на практике.

Использование оператора LOG

Оператор LOG относится к категории математических функций. Его задачей является вычисление логарифма указанного числа по заданному основанию. Синтаксис у указанного оператора предельно простой:

Как видим, функция располагает всего двумя аргументами.

Аргумент «Число» представляет собой число, из которого нужно вычислить логарифм. Он может принимать вид числового значения и являться ссылкой на ячейку, его содержащую.

Аргумент «Основание» представляет собой основание, по которому будет вычисляться логарифм. Он тоже может иметь, как числовой вид, так и выступать в виде ссылки на ячейку. Данный аргумент не является обязательным. Если он опущен, то считается, что основание равно нулю.

Кроме того, в Экселе существует ещё одна функция, позволяющая вычислять логарифмы – LOG10. Её главное отличие от предыдущей в том, что она может вычислять логарифмы исключительно по основанию 10, то есть, только десятичные логарифмы. Её синтаксис ещё проще, чем у ранее представленного оператора:

Как видим, единственным аргументом данной функции является «Число», то есть, числовое значение или ссылка на ячейку, в которой оно расположено. В отличие от оператора LOG у этой функции аргумент «Основание» вообще отсутствует, так как принимается, что основание обрабатываемых ею значений равно 10.

Способ 1: применение функции LOG

Теперь давайте рассмотрим применение оператора LOG на конкретном примере. Имеем столбец числовых значений. Нам нужно вычислить из них логарифм по основанию 5.

1. Выполняем выделение первой пустой ячейки на листе в колонке, в которую планируем выводить итоговый результат. Далее щелкаем по пиктограмме «Вставить функцию», которая располагается возле строки формул.

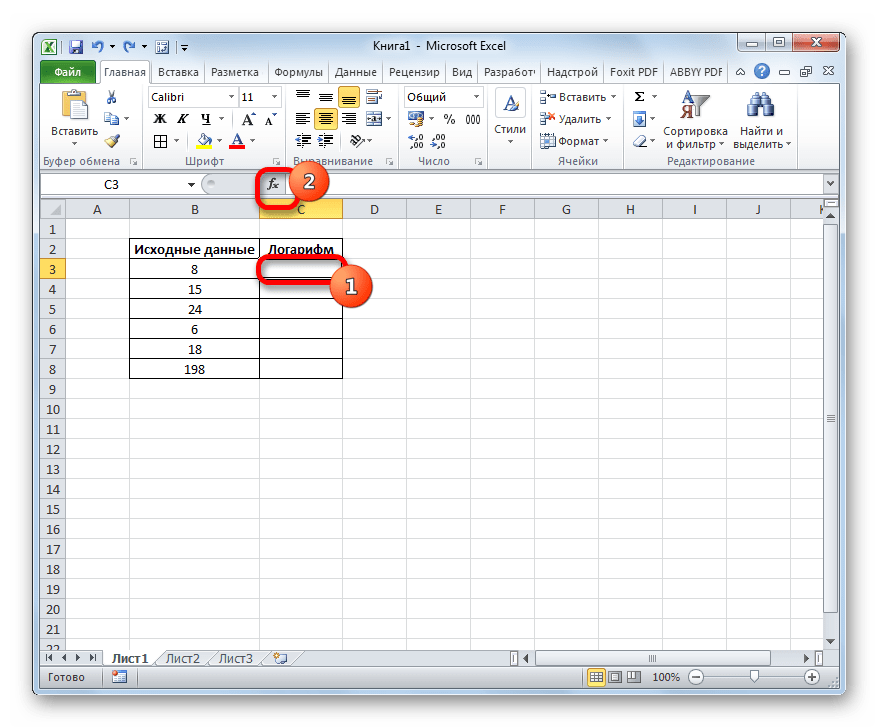
Происходит запуск окошка Мастера функций. Перемещаемся в категорию «Математические». Производим выделение наименования «LOG» в списке операторов, после чего производим щелчок по кнопке «OK».

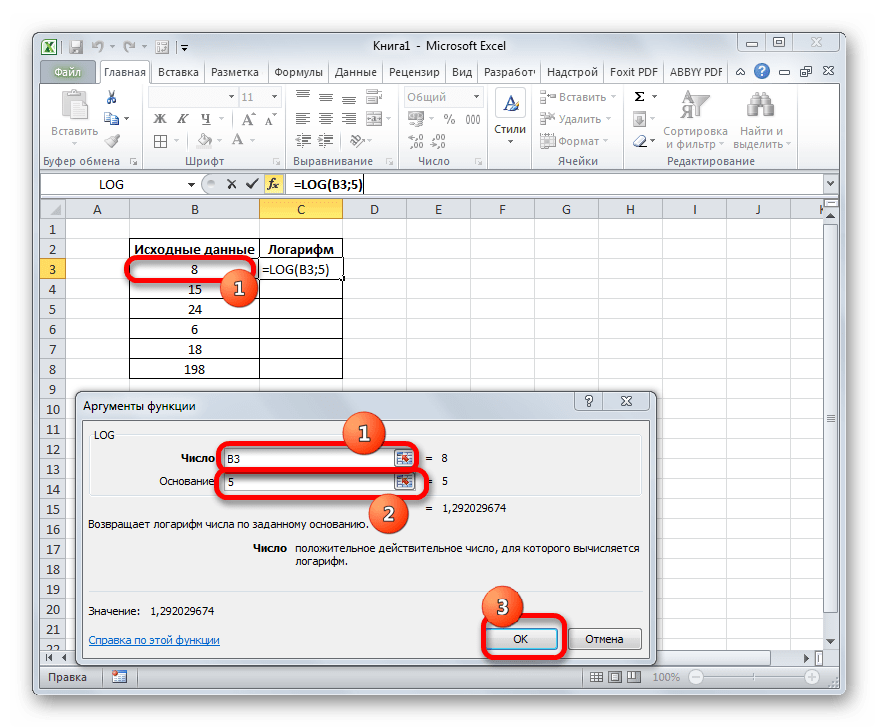
Происходит запуск окошка аргументов функции LOG. Как видим, оно имеет два поля, которые соответствуют аргументам данного оператора.

В поле «Число» в нашем случае следует ввести адрес первой ячейки того столбца, в котором находятся исходные данные. Это можно сделать, вписав его в поле вручную. Но существует и более удобный способ. Устанавливаем курсор в указанном поле, а затем щелкаем левой кнопкой мыши по ячейке таблицы, содержащей нужное нам числовое значение. Координаты данной ячейки тут же отобразятся в поле «Число».

В поле «Основание» просто вписываем значение «5», так как оно будет одинаково для всего обрабатываемого числового ряда.

После произведения указанных манипуляций щелкаем по кнопке «OK».

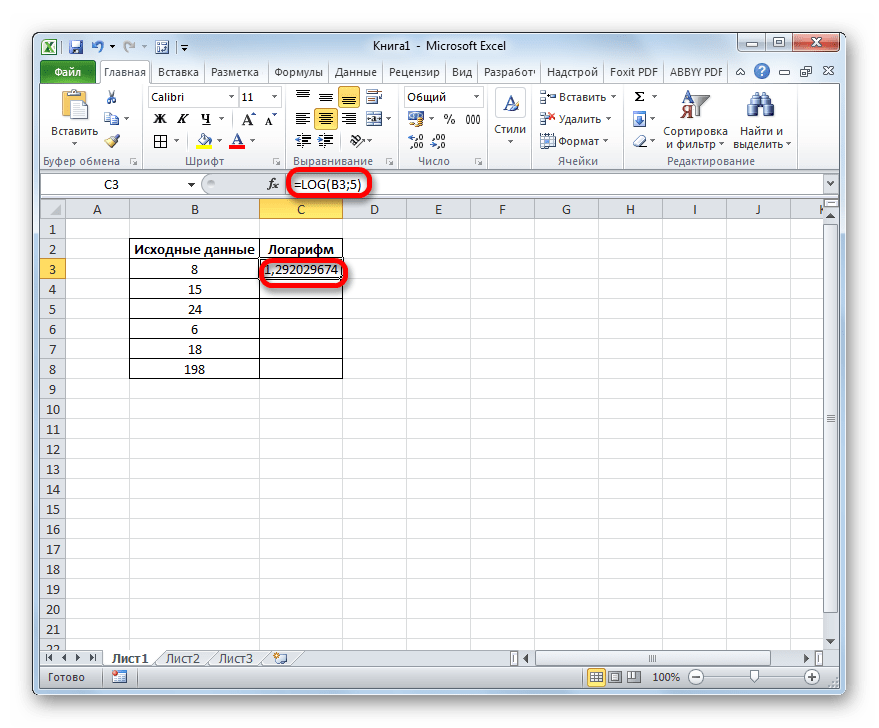
Результат обработки функцией LOG тут же выводится в ячейку, указанную нами на первом шаге этой инструкции.

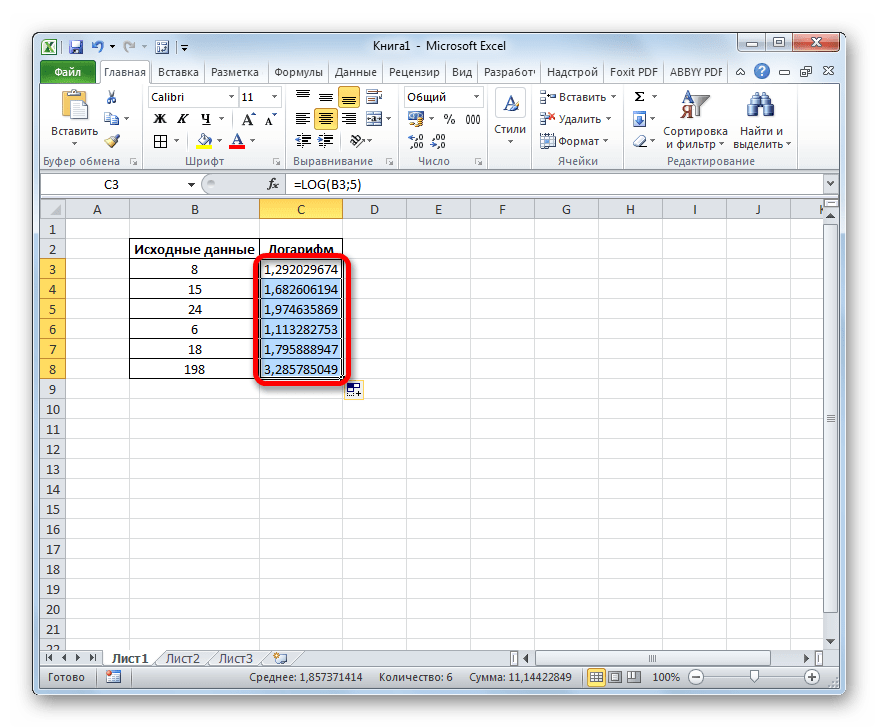
Но мы заполнили только первую ячейку столбца. Для того, чтобы заполнить и остальные, нужно скопировать формулу. Устанавливаем курсор в нижний правый угол ячейки её содержащей. Появляется маркер заполнения, представ в виде крестика. Выполняем зажим левой кнопки мыши и перетягиваем крестик до конца столбца.

Способ 2: применение функции LOG10

Теперь давайте рассмотрим пример использования оператора LOG10. Для примера возьмем таблицу с теми же исходными данными. Но теперь, понятное дело, предстоит задача вычислить логарифм чисел, расположенных в столбце «Исходные данные» по основанию 10 (десятичный логарифм).

Производим выделение первой пустой ячейки столбца «Логарифм» и щелкаем по пиктограмме «Вставить функцию».

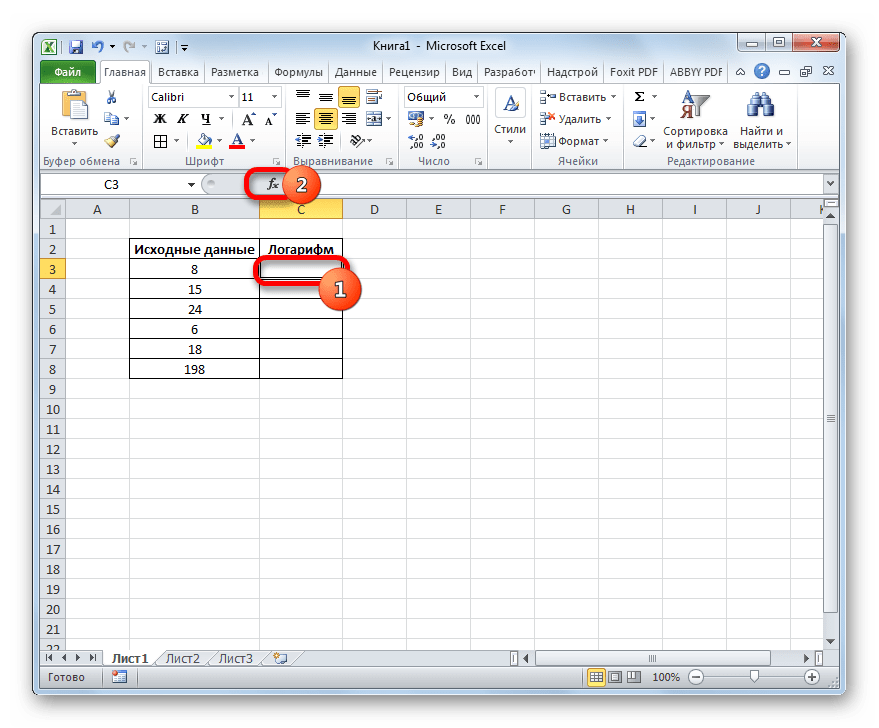
В открывшемся окне Мастера функций опять выполняем переход в категорию «Математические», но на этот раз останавливаемся на наименовании «LOG10». Щелкаем внизу окошка по кнопке «OK».

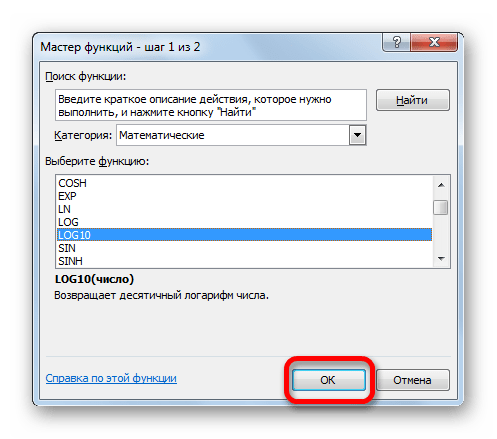
Происходит активация окна аргументов функции LOG10. Как видим, оно располагает только одним полем – «Число». Вносим в него адрес первой ячейки столбца «Исходные данные», тем же способом, который мы использовали в предыдущем примере. Затем щелкаем по кнопке «OK» внизу окна.

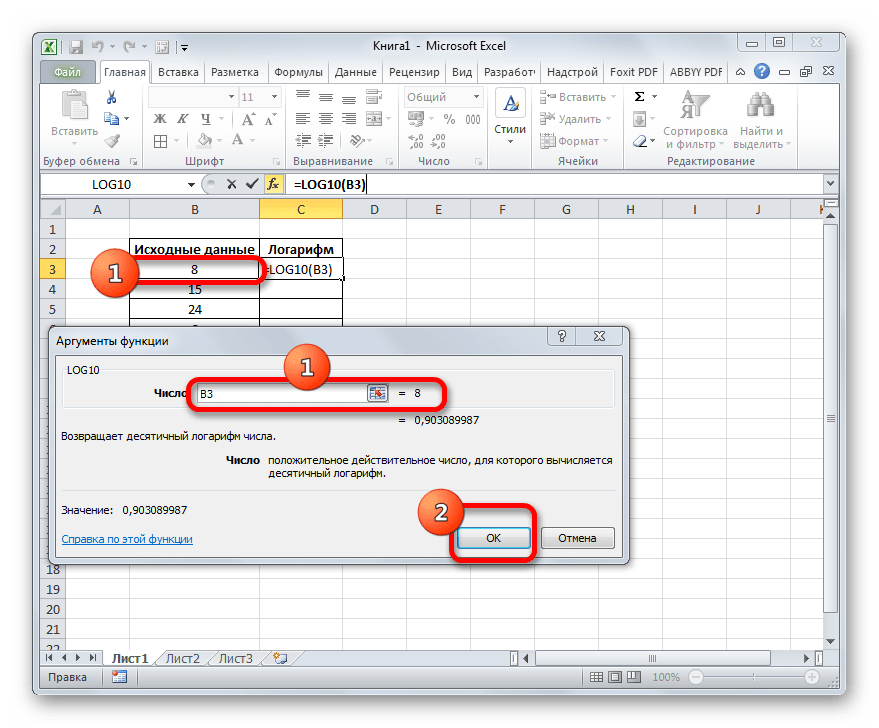
Результат обработки данных, а именно десятичный логарифм заданного числа, выводится в предварительно указанную ячейку.

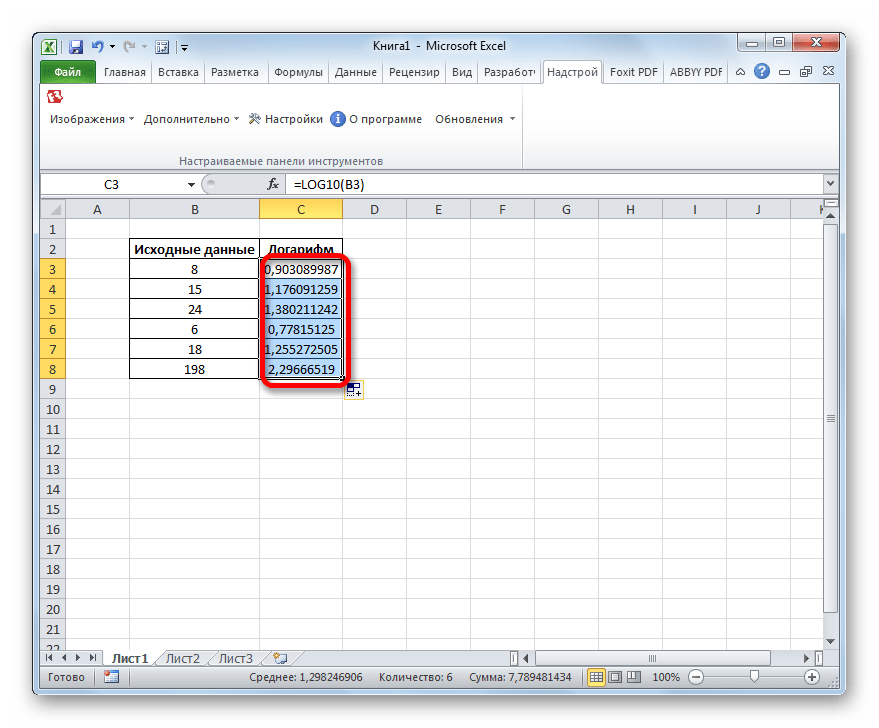
Применение функции LOG позволяет в Экселе просто и быстро посчитать логарифм от указанного числа по заданному основанию. Этот же оператор может посчитать и десятичный логарифм, но для указанных целей более рационально использовать функцию LOG10.

Отблагодарите автора, поделитесь статьей в социальных сетях.

В этой статье описан синтаксис формулы и использование функции LN в Microsoft Excel.

Описание

Возвращает натуральный логарифм числа. Натуральный логарифм — это логарифм по основанию e (2,71828182845904).

Синтаксис

Аргументы функции LN описаны ниже.

Число Обязательный. Положительное вещественное число, для которого вычисляется натуральный логарифм.

Замечание

LN является обратной функцией к EXP.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Натуральный логарифм числа 86

Натуральный логарифм числа e

Натуральный логарифм числа e, возведенного в третью степень

Функция LN в Excel предназначена для расчета натурального логарифма числа и возвращает соответствующее числовое значение. Натуральным логарифмом является логарифм с основанием e (число Эйлера, равное примерно 2,718).

Функция LOG в Excel используется для расчета логарифма числа, при этом основание логарифма может быть указано явно в качестве второго аргумента данной функции.

Функция LOG10 в Excel предназначена для расчета логарифма числа с основанием 10 (десятичный логарифм).

Примеры использования функций LN, LOG и LOG10 в Excel

Пример 1. Археологи нашли останки древнего животного. Для определения их возраста было решено воспользоваться методом радиоуглеродного анализа. В результате замеров оказалось, что содержание радиоактивного изотопа C 14 составило 17% от количества, которое обычно содержится в живых организмах. Рассчитать возраст останков, если период полураспада изотопа углерода 14 составляет 5760 лет.

Вид исходной таблицы:

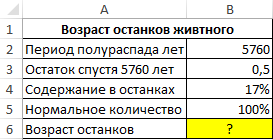
Для решения используем следующую формулу:

Данная формула была получена на основе формулы x=t*(lgB-lgq)/lgp, где:

• q – количество изотопа углерода в начальный момент (в момент смерти животного), выраженное единицей (или 100%);
• B – количество изотопа в момент проведения анализа останков;
• t – период полураспада изотопа;
• p – числовое значение, указывающее, во сколько раз изменяется количество вещества (изотопа углерода) за период времени t.

В результате вычислений получим:

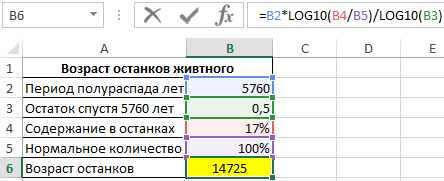
Найденным останкам почти 15 тыс. лет.

Депозитный калькулятор со сложным процентом в Excel

Пример 2. Клиент банка внес депозит на сумму 50000 рублей с процентной ставкой 14,5% (сложные проценты). Определить, сколько времени потребуется на удвоение вложенной суммы?

Интересный факт! Для быстрого решения данной задачи можно воспользоваться эмпирическим способом приблизительной оценки сроков (в годах) на удвоение инвестиций, вложенных под сложный процент. Так называемое правило 72 (или 70 или правило 69). Для этого нужно воспользоваться простой формулой – число 72 разделить на процентную ставку: 72/14,5 = 4,9655 лет. Главный недостаток правила «магического» числа 72 заключается в погрешности. Чем выше процентная ставка, тем выше погрешность в правиле 72. Например, при процентной ставки 100% годовых погрешность в годах достигает до 0,72 (а в процентах это аж 28%!).

Для точного расчета сроков удвоения инвестиций будем использовать функцию LOG. За одно и проверим величину погрешности правила 72 при процентной ставке 14,5% годовых.

Вид исходной таблицы:

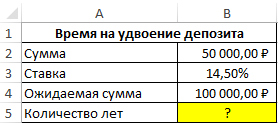
Для расчета будущей стоимости инвестиции при известной процентной ставке можно использовать следующую формулу: S=A(100%+n%) t , где:

• S – ожидаемая сумма по истечению срока;
• A – размер депозита;
• n – процентная ставка;
• t – срок хранения депозитных средств в банке.

Для данного примера эту формулу можно записать как 100000=50000*(100%+14,5%) t или 2=(100%+14,5%) t . Тогда для нахождения t можно переписать уравнение как t=log_(114,5%)2 или t=log_1,1452.

Для нахождения значения t запишем следующую формулу сложного процента по депозиту в Excel:

• B4/B2 – соотношение ожидаемой и начальной сумм, которое является показателем логарифма;
• 1+B3 – прирост процентов (основание логарифма).

В результате расчетов получим:

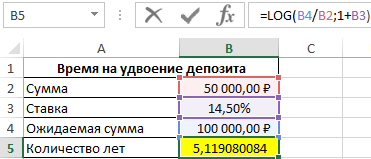
Депозит удвоится спустя немного более чем 5 лет. Для точного определения лет и месяцев воспользуемся формулой:

Функция ОТБР отбрасывает в дробном числе все что после запятой подобно функции ЦЕЛОЕ. Разница между функциями ОТБР и ЦЕЛОЕ заключается лишь в расчетах с отрицательными дробными числами. Кроме того, ОТБР имеет второй аргумент где можно указать количество оставляемых знаков после запятой. Поэтом в данном случаи можно воспользоваться любой из этих двух функций на выбор пользователя.

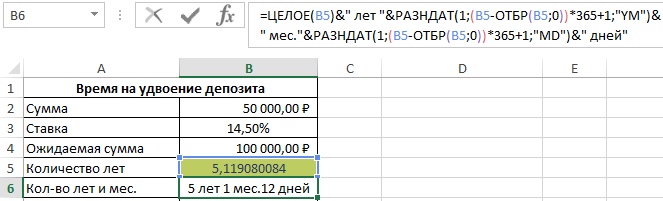
Получилось 5 лет и 1 месяц и 12 дней. Теперь сравним точные результаты с правилом 72 и определим величину погрешности. Для данного примера формула, следующая:

Мы должны умножить значение ячейки B3 на 100 так как ее текущее значение 0,145, которое отображается в процентном формате. В результате:

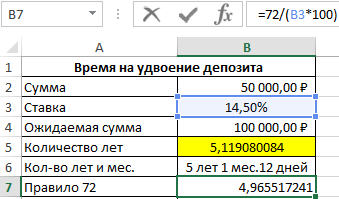
После скопируем формулу из ячейки B6 в ячейку B8, а в ячейке B9:

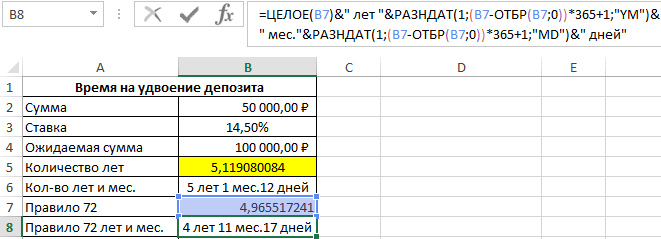
Посчитаем сроки погрешности:

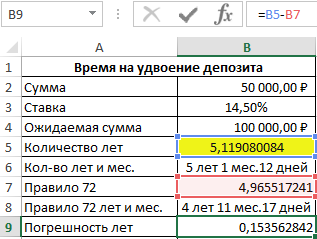
Затем в ячейку B10 снова скопируем формулу из ячейки B6. В результате получим разницу:

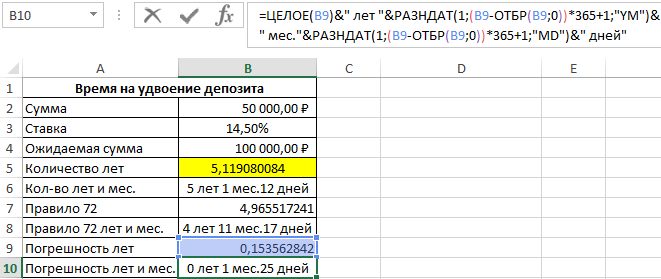
И наконец посчитаем разницу в процентах, чтобы проверить как изменяется размер отклонения и насколько существенно влияет рост процентной ставки на уровень расхождения правила 72 и факта:

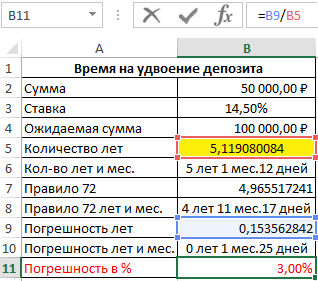
Теперь для наглядности пропорциональной зависимости роста погрешности и роста уровня процентной ставки повысим процентную ставку до 100% годовых:

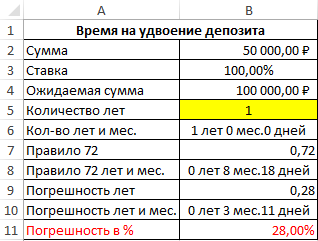
На первый взгляд разница погрешности не существенная по сравнению с 14,5% годовых — всего около 2-ух месяцев и 100% годовых — в пределах 3-х месяцев. Но доля погрешности в сроках окупаемости более чем ¼, а точнее 28%.

Составим простой график для визуального анализа как коррелируется зависимость изменения процентной ставки и процента погрешности правила 72 от факта:

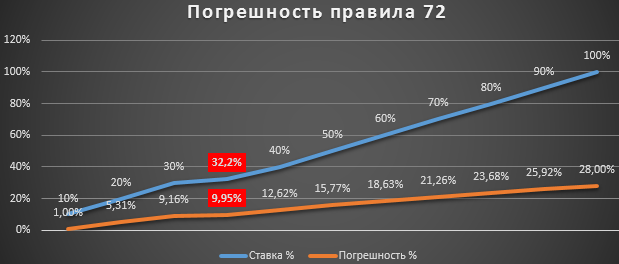
Чем выше процентная ставка, тем хуже работает правило 72. В итоге можно сделать следующий вывод: до 32,2% процентов годовых можно смело пользоваться правилом 72. Тогда погрешность составляет менее 10-ти процентов. Вполне сойдет если не требуются точные, но сложные расчеты по срокам окупаемости инвестиций в 2 раза.

Инвестиционный калькулятор сложных процентов с капитализацией в Excel

Пример 3. Клиенту банка предложили сделать вклад с непрерывным ростом итоговой суммы (капитализация со сложными процентами). Процентная ставка составляет 13% годовых. Определить, сколько потребуется времени, чтобы утроить начальную сумму (250000 рублей). Насколько необходимо увеличить процентную ставку, чтобы уменьшить время ожидания вдвое?

Примечание: так как мы в данном примере утраиваем сумму вложений, то здесь уже правило 72 не работает.

Вид исходной таблицы данных:

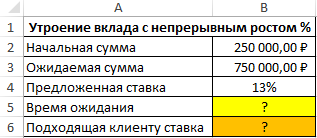
Непрерывный рост может быть описан формулой ln(N)=p*t, где:

• N – отношение конечной суммы вклада к начальной;
• p – процентная ставка;
• t – количество лет, прошедших с момента внесения депозита.

Тогда t=ln(N)/p. Исходя из этого равенства запишем формулу в Excel:

• B3/B2 – соотношение конечной и начальной сумм депозита;
• B4 – процентная ставка.

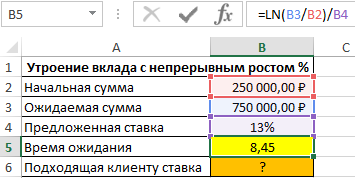
На утроение начальной суммы вклада потребуется почти 8,5 лет. Для расчета ставки, которая позволит сократить время ожидания вдвое, используем формулу:

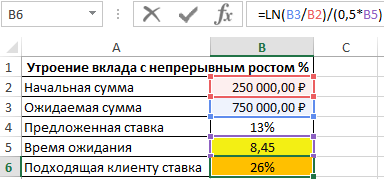
То есть, необходимо удвоить начальную процентную ставку.

Особенности использования функций LN, LOG и LOG10 в Excel

Функция LN имеет следующий синтаксис:

• число – единственный аргумент, являющийся обязательным для заполнения, который принимает действительные числа из диапазона положительных значений.

1. Функция LN является обратной функцией EXP. Последняя возвращает значение, полученное в результате возведения числа e в указанную степень. Функция LN указывает, в какую степень необходимо возвести число e (основание), чтобы получить показатель логарифма (аргумент число).
2. Если аргумент число задан числом из диапазона отрицательных значений или нулем, результатом выполнения функции LN будет код ошибки #ЧИСЛО!.

Синтаксис функции LOG имеет следующий вид:

=LOG( число ;[основание])

• число – обязательный для заполнения аргумент, характеризующий числовое значение показателя логарифма, то есть число, полученное в результате возведения основания логарифма в некоторую степень, которая и будет вычислена функцией LOG;
• [основание] – необязательный для заполнения аргумент, характеризующий числовое значение основания логарифма. Если аргумент явно не указан, логарифм считается десятичным (то есть основание равно 10).

1. Несмотря на то, что результат вычисления функции LOG может являться отрицательным числом (например, функция =LOG(2;0,25) вернет значение -0,5), аргументы данной функции должны быть взяты из диапазона положительных значений. Если хотя бы один из аргументов является отрицательным числом, функция LOG вернет код ошибки #ЧИСЛО!.
2. Если в качестве аргумента [основание] было передано значение 1, функция LOG вернет код ошибки #ДЕЛ/0!, поскольку результат возведения 1 в любую степень будет всегда одинаковым и равным 1.

Функция LOG10 имеет следующую синтаксическую запись:

• число – единственный и обязательный для заполнения аргумент, смысл которого тождественен одноименному аргументу функций LN и LOG.

Примечание: если в качестве аргумента число было передано отрицательное число или 0, функция LOG10 вернет код ошибки #ЧИСЛО!.