Как найти угол под которым пересекаются кривые
Содержание
Читайте также:
- II. Операционная стратегия на примере отдельного предприятия.
- PEST-анализ и пример его использования
- SWOT-анализ и пример его использования
- VI. ПРИМЕРНЫЙ ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ ПО ПОДГОТОВКЕ К ЭКЗАМЕНУ
- А Примерный перечень вопросов, рассматриваемых на практических занятиях
- А. Работа переписчиков на Руси. Причины и примеры порчи текста в древнеславянских рукописях библейских книг.
- А.2. Пример описания объекта
- Анализ примера
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 1 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 2 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 3 страница
- Аппаратная поддержка мультипрограммирования на примере процессора Pentium 4 страница
Решение.Найдем точки пересечения кривых, решив систему уравнений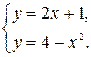
Отсюда имеем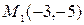 
, 
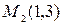. Далее, определим угловые коэффициенты касательных к параболе в точках 
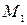и 
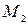.Соответственно имеем 
, 
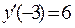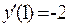. Угловой коэффициент прямой во всех точках один и тот же и равен в нашем случае 2. Далее находим углы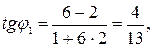 
,
.
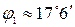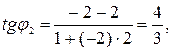
Пример 3.Определить в каких точках заданной линии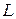 
касательная к этой линии параллельна прямой 
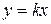и написать уравнение этой касательной
, 
.
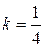Решение. Находим производную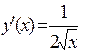 
. Далее находим значение 
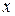из уравнения 
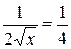. Имеем, 
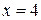.Значения функции 
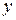при 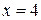есть 
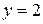и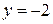 
. Отсюда имеем, 
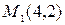и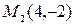 
точки заданной линии 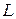в которых касательная к этой линии параллельна данной прямой 
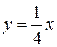. Найдем теперь уравнения этих касательных. Используя формулу (1), получим
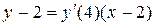-уравнение касательной в точке ,
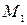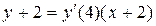-уравнение касательной в точке .
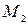Контрольные вопросы.
1.Геометрический смысл производной.
2.Касательная и нормаль к кривой.
3.Угол между двумя кривыми.
4.Другие приложения производной.
Задания.
1.Найти углы, под которыми пересекаются эллипс и парабола
, 
.
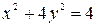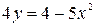2. Определить в каких точках заданной линии 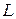касательная к этой линии параллельна прямой 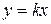и написать уравнение этой касательной
1) 
, 
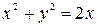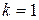; 2) 
, 
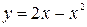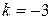; 3)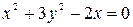 
, 
.
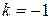3.Найти угол между кривой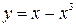 
и прямой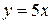 
Дата добавления: 2014-12-16 ; Просмотров: 3162 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Планиметрические задачи
Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если:
Решение. Уравнение касательной будем искать по формуле ; уравнение нормали — по формуле По условию, .
Подставляем все найденные значения в уравнение касательной:
Теперь находим уравнение нормали:
Ответ: уравнение касательной:; уравнение нормали:
Задача 2.Написать уравнения касательной и нормали в точке
Подставим полученные решения в равенство
Найдем производную функции, заданной параметрически .
Подставляем все найденные значение в уравнение касательной:
Теперь находим уравнение нормали:
Ответ: уравнение касательной: уравнение нормали: .
Задача 3. Найти углы, под которыми пересекаются заданные кривые:
Решение. Угол между кривыми находится по формуле
Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:
Таким образом, кривые пересекаются в точках .
Далее найдем значения производных заданных функций в точках пересечения.
производный дифференцирование уравнение планиметрический
Подставляем найденные значение в формулу нахождения угла:
Ответ: в точке угол равен 0 (т.е. касательные совпадают), в точке угол равен .
Задача 4. Задан прямоугольник с периметром 56 см. Каковы должны быть его стороны, чтобы площадь была наибольшей [7]?
Обозначим одну из сторон за, тогда вторая сторона:
Площадь такого прямоугольника составит:
Требуется найти максимум функции .
Это квадратичная функция, ее график — парабола, ветви которой направлены вниз.
Определим критические точки: .
Так, — точка экстремума, слева от нее производная положительна, а справа — отрицательна.
Очевидно, что — точка максимума. В таком случае площадь прямоугольника максимальна, когда его стороны равны 14 см, то есть когда он является квадратом.
Ответ: площадь максимальна, когда стороны прямоугольника равны 14 см.
Задача 5. Площадь прямоугольника составляет . Каковы должны быть его размеры этого прямоугольника, чтобы периметр был минимальным?[7]
Пусть стороны прямоугольника равны . Тогда:
Периметр такого прямоугольника составит:
Требуется найти минимум данной функции. Найдём производную:
Найдем точки экстремума:
Очевидно, что , поэтому нас интересует точка .Слева от нее производная отрицательна, а справа — положительна.
Так, — точка минимума.
Ответ: чтобы периметр прямоугольника был минимальным, его стороны должны составить 4 см.
Задача 6. Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне. Найти условия, при которых площадь параллелограмма является наибольшей [2].
Пусть треугольник определяется двумя сторонами и углом между ними (рис.4). Построим параллелограмм в соответствии с условиями задачи. Обозначим стороны параллелограмма Площадь параллелограмма определяется формулой
Выразим через и стороны треугольника . Из подобия треугольников и следует, что
В результате площадь записывается как функция:
Отсюда видно, что экстремум функциисуществует в следующей точке:
При переходе через эту точку производная меняет свой знак с плюса на минус, то есть эта точка является точкой максимума. Другая сторона параллелограмма при этом равна
Итак, вписанный в треугольник параллелограмм со сторонами имеет наибольшую площадь при условии
где стороны треугольника. Интересно, что результат не зависит от угла между сторонами треугольника.
Ответ: площадь параллелограмма является наибольшей при условии
где стороны треугольника.
Задача 7.Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром [2].
Пусть треугольник вписан в окружность данного радиуса ,
(независимая переменная) (рис.5). Выразим периметр треугольника как функцию . По теореме синусов:
. Найдем, при каком значении функция принимает наибольшее значение на данном интервале
следовательно, точка максимума, в которой функция принимает наибольшее значение на заданном промежутке. Таким образом, наибольший периметр имеет равносторонний треугольник.
Ответ: среди всех равнобедренных треугольник, вписанных в данную окружность, с наибольшим периметром является равносторонний треугольник.
Задача 8.Окно имеет форму прямоугольника, ограниченного сверху полукругом.
Периметр окна равен . Определить радиус полукруга , при котором площадь окна является наибольшей (рис.6) [2].
Очевидно, что одна сторона прямоугольника равна . Другую сторону обозначим через . Периметр всего окна выражается формулой
Площадь окна составляет:
Полученное выражение представляет собой функцию . Исследуем ее на экстремум. Находим производную:
Определяем стационарные точки:
Поскольку вторая производная отрицательна:
то найденная точка является точкой максимума, т.е. при этом значении площадь окна будет наибольшей.
Само максимальное значение площади составляет
Ответ: радиус полукруга , при котором площадь является наибольшей.
Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — сделанный для людей. Все решебники выполнены качественно, с приятной навигацией. Вы сможете скачать гдз, решебник английского, улучшить ваши школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам в решении домашнего задания. Кроме того, весь материал гдз совершенствуется, добавляются новые сборники решений.
Информация
© admin
reshak.ru
Загрузка...