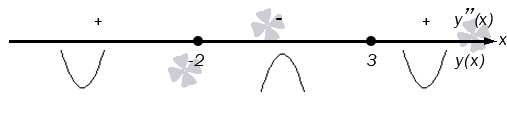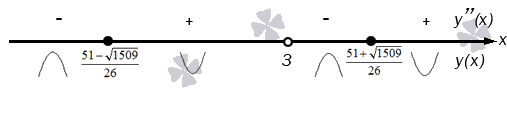Найдем производные до третьего порядка фунции, указанной в условии к задаче:
$$ y'(x) = (cos x)’ = — sin x $$ $$ y»(x) = (-sin x)’ = -cos x $$ $$ y»'(x) = (-cos x)’ = sin x $$
Вычислим значения $ y»(x_0) ext < и >y»'(x_0) $:
Так как $ y»(frac<pi><2>) = 0 $, а $ y»'(frac<pi><2>)
eq 0 $, то делаем вывод, что точка $ x_0 = frac<pi> <2>$ является точкой перегиба для функции $ y = cos x $
Направление выпуклости графика функции. Точки перегиба
Определение : Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
Определение : Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x) , характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) Определение: Точка графика функции y=f(x) , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
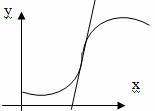
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x) , в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x) .
- Найти критические точки II рода функции y=f(x) , т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x) . Если при этом критическая точка x разделяет промежутки выпуклости противоположных направлений, то x является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1 . Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x 2 –x 3 .
Решение: Находим f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0 . x=2 .

f(2) = 6*2 2 – 2 3 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞) ; функция выпукла вниз при x∈(-∞; 2) ; точка перегиба (2;16) .
Пример 2 . Имеет ли точки перегиба функция: f(x)=x 3 -6x 2 +2x-1
Пример 3 . Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x 3 -6x 2 +12x+4
Когда мы чертим график функции, важно определить интервалы выпуклости и точки перегиба. Они, наряду с промежутками убывания и возрастания, нужны нам для четкого представления функции в графическом виде.
Понимание этой темы требует знания того, что такое производная функции и как ее вычислить до некоторого порядка, а также умения решать разные виды неравенств.
В начале статьи определяются основные понятия. Потом мы покажем, какая связь существует между направлением выпуклости и значением второй производной на определенном интервале. Далее мы укажем условия, в которых можно определить точки перегиба графика. Все рассуждения будут проиллюстрированы примерами решений задач.
Что такое выпуклость/вогнутость функции и точки перегиба графика функции
Дифференцируемая функция является выпуклой по направлению вниз на некотором интервале в том случае, когда ее график располагается не ниже касательной к нему в любой точке этого интервала.
Дифференцируемая функция является выпуклой по направлению вверх на некотором интервале в том случае, если график данной функции располагается не выше касательной к нему в любой точке этого интервала.
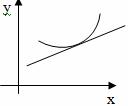
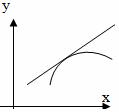
Выпуклую вниз функцию можно иначе назвать вогнутой. Оба определения наглядно показаны на графике ниже:
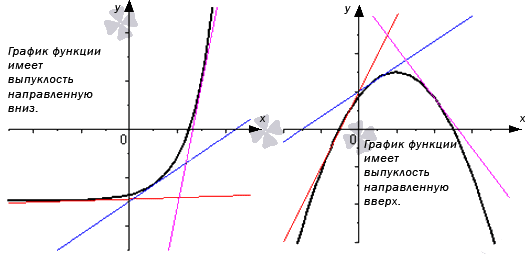
Точка перегиба функции – это точка M ( x 0 ; f ( x 0 ) ) , в которой существует касательная к графику функции, при условии существования производной в окрестности точки x 0 , где с левой и правой стороны график функции принимает разные направления выпуклости.
Проще говоря, точка перегиба – это место на графике, в котором есть касательная, и направление выпуклости графика при прохождении через это место будет менять направление выпуклости. Если вы не помните, при каких условиях возможно существование вертикальной и невертикальной касательной, советуем повторить раздел о касательной графика функции в точке.
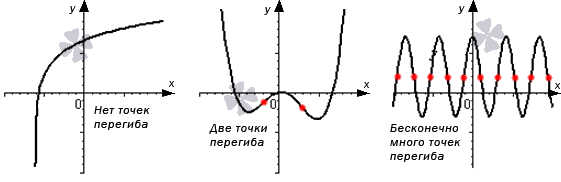
Ниже указан график функции, имеющей несколько точек перегиба, которые выделены красным. Уточним, что наличие точек перегиба не является обязательным. На графике одной функции их может быть одна, две, несколько, бесконечно много или ни одной.
Как найти интервалы выпуклости функции
В этом пункте мы расскажем о теореме, с помощью которой можно определить промежутки выпуклости на графике конкретной функции.
График функции будет иметь выпуклость по направлению вниз или вверх в том случае, если у соответствующей ему функции y = f ( x ) будет вторая конечная производная на указанном интервале x при условии, что неравенство f » ( x ) ≥ 0 ∀ x ∈ X ( f » ( x ) ≤ 0 ∀ x ∈ X ) будет верным.
Используя данную теорему, можно найти промежутки вогнутости и выпуклости на любом графике функции. Для этого нужно просто решить неравенства f » ( x ) ≥ 0 и f » ( x ) ≤ 0 на области определения соответствующей функции.
Уточним, что те точки, в которых вторая производная не существует, но функция y = f ( x ) определена, будут включаться в интервалы выпуклости и вогнутости.
Посмотрим на примере конкретной задачи, как правильно применять эту теорему.
Условие: дана функция y = x 3 6 — x 2 + 3 x — 1 . Определите, на каких промежутках ее график будет иметь выпуклости и вогнутости.
Решение
Областью определения данной функции является все множество действительных чисел. Начнем с вычисления второй производной.
y ‘ = x 3 6 — x 2 + 3 x — 1 ‘ = x 2 2 — 2 x + 3 ⇒ y ‘ ‘ = x 2 2 — 2 x + 3 = x — 2
Мы видим, что область определения второй производной совпала с областью самой функции Значит, для выявления интервалов выпуклостей нам надо решить неравенства f » ( x ) ≥ 0 и f » ( x ) ≤ 0 .
y » ≥ 0 ⇔ x — 2 ≥ 0 ⇔ x ≥ 2 y » ≤ 0 ⇔ x — 2 ≤ 0 ⇔ x ≤ 2
Мы получили, что график заданной функции будет иметь вогнутость на отрезке [ 2 ; + ∞ ) и выпуклость на отрезке ( — ∞ ; 2 ] .
Для наглядности изобразим график функции и отметим на нем выпуклую часть синим, а вогнутую – красным цветом.
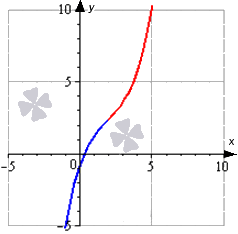
Ответ: график заданной функции будет иметь вогнутость на отрезке [ 2 ; + ∞ ) и выпуклость на отрезке ( — ∞ ; 2 ] .
А что же делать в случае, если область определения второй производной не совпадает с областью определения функции? Здесь нам пригодится замечание, сделанное выше: те точки, где конечная вторая производная не существует, мы тоже будем включать в отрезки вогнутости и выпуклости.
Условие: дана функция y = 8 x x — 1 . Определите, в каких промежутках ее график будет иметь вогнутость, а в каких – выпуклость.
Решение
Для начала выясним область определения функции.
x ≥ 0 x — 1 ≠ 0 ⇔ x ≥ 0 x ≠ 1 ⇔ x ∈ [ 0 ; 1 ) ∪ ( 1 ; + ∞ )
Теперь вычисляем вторую производную:
y ‘ = 8 x x — 1 ‘ = 8 · 1 2 x · ( x — 1 ) — x · 1 ( x — 1 ) 2 = — 4 · x + 1 x · ( x — 1 ) 2 y » = — 4 · x + 1 x · ( x — 1 ) 2 ‘ = — 4 · 1 · x · x — 1 2 — ( x + 1 ) · x · x — 1 2 ‘ x · ( x — 1 ) 4 = = — 4 · 1 · x · x — 1 2 — x + 1 · 1 2 x · ( x — 1 ) 2 + x · 2 ( x — 1 ) x · x — 1 4 = = 2 · 3 x 2 + 6 x — 1 x 3 2 · ( x — 1 ) 3
Область определения второй производной – это множество x ∈ ( 0 ; 1 ) ∪ ( 1 ; + ∞ ) . Мы видим, что x , равный нулю, будет принадлежать области определения исходной функции, но не области определения второй производной. Эту точку нужно обязательно включить в отрезок вогнутости или выпуклости.
После этого нам надо решить неравенства f » ( x ) ≥ 0 и f » ( x ) ≤ 0 на области определения заданной функции. Используем для этого метод интервалов: при x = — 1 — 2 3 3 ≈ — 2 , 1547 или x = — 1 + 2 3 3 ≈ 0 , 1547 числитель 2 · ( 3 x 2 + 6 x — 1 ) x 2 3 · x — 1 3 обращается в 0 , а знаменатель равен 0 при x , равном нулю или единице.
Нанесем получившиеся точки на график и определим знак выражения на всех интервалах, которые войдут в область определения исходной функции. На графике эта область обозначена штриховкой. Если значение положительно, отмечаем интервал плюсом, если отрицательно, то минусом.

f » ( x ) ≥ 0 x ∈ [ 0 ; 1 ) ∪ ( 1 ; + ∞ ) ⇔ x ∈ 0 ; — 1 + 2 3 3 ∪ ( 1 ; + ∞ ) , а f » ( x ) ≤ 0 x ∈ [ 0 ; 1 ) ∪ ( 1 ; + ∞ ) ⇔ x ∈ [ — 1 + 2 3 3 ; 1 )
Включаем ранее отмеченную точку x = 0 и получаем нужный ответ. График исходной функции будет иметь выпуклость по направлению вниз при 0 ; — 1 + 2 3 3 ∪ ( 1 ; + ∞ ) , и вверх – при x ∈ [ — 1 + 2 3 3 ; 1 ) .
Изобразим график, отметив на нем выпуклую часть синим, а вогнутую красным цветом. Вертикальная асимптота отмечена черным пунктиром.
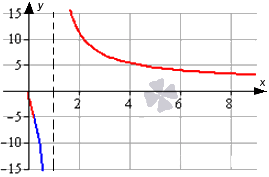
Ответ: График исходной функции будет иметь выпуклость по направлению вниз при 0 ; — 1 + 2 3 3 ∪ ( 1 ; + ∞ ) , и вверх – при x ∈ [ — 1 + 2 3 3 ; 1 ) .
Условия перегиба графика функции
Начнем с формулировки необходимого условия перегиба графика некоторой функции.
Допустим, что у нас есть функция y = f ( x ) , график которой имеет точку перегиба. При x = x 0 у него есть непрерывная вторая производная, следовательно, будет выполняться равенство f » ( x 0 ) = 0 .
Учитывая данное условие, нам следует поискать точки перегиба среди тех, в которых вторая производная будет обращаться в 0 . Это условие не будет достаточным: не все такие точки нам подойдут.
Также обратите внимание, что, согласно общему определению, нам нужна будет касательная прямая, вертикальная или невертикальная. На практике это означает, что для нахождения точек перегиба следует взять те, в которых вторая производная данной функции обращается в 0 . Следовательно, чтобы найти абсциссы точек перегиба, нам нужно взять все x 0 из области определения функции, где lim x → x 0 — 0 f ‘ ( x ) = ∞ и lim x → x 0 + 0 f ‘ ( x ) = ∞ . Чаще всего это такие точки, в которых знаменатель первой производной обращается в 0 .
Первое достаточное условие существования точки перегиба графика функции
Мы нашли все значения x 0 , которые можно взять в качестве абсцисс точек перегиба. После этого нам нужно применить первое достаточное условие перегиба.
Допустим, что у нас есть функция y = f ( x ) , которая является непрерывной в точке M ( x 0 ; f ( x 0 ) ) . При этом она имеет на этой точке касательную, а сама функция имеет вторую производную в окрестности этой точки x 0 . В таком случае если с левой и правой стороны вторая производная приобретает противоположные знаки, то данную точку можно считать точкой перегиба.
Мы видим, что данное условие не требует, что в этой точке непременно существовала вторая производная, достаточно ее наличия в окрестности точки x 0 .
Все сказанное выше удобно представить в виде последовательности действий.
Как найти точки перегиба графика функции
- Для начала нужно найти все абсциссы x 0 возможных точек перегиба, где f » ( x 0 ) = 0 , lim x → x 0 — 0 f ‘ ( x ) = ∞ , lim x → x 0 + 0 f ‘ ( x ) = ∞ .
- Выясним, в каких точках производная будет менять знак. Эти значения и есть абсциссы точек перегиба, а точки M ( x 0 ; f ( x 0 ) ) , соответствующие им, – это сами точки перегиба.
Для наглядности разберем две задачи.
Условие: дана функция y = 1 10 · x 4 12 — x 3 6 — 3 x 2 + 2 x . Определите, где график данной функции будет иметь точки перегиба и выпуклости.
Решение
Указанная функция определена на всем множестве действительных чисел. Считаем первую производную:
y ‘ = 1 10 · x 4 12 — x 3 6 — 3 x 2 + 2 x ‘ = 1 10 · 4 x 3 12 — 3 x 2 6 — 6 x + 2 = = 1 10 · x 3 3 — x 2 2 — 6 x + 2
Теперь найдем область определения первой производной. Это также множество всех действительных чисел. Значит, равенства lim x → x 0 — 0 f ‘ ( x ) = ∞ и lim x → x 0 + 0 f ‘ ( x ) = ∞ не могут быть выполнены ни при каких значениях x 0 .
Вычисляем вторую производную:
y ‘ ‘ = = 1 10 · x 3 3 — x 2 2 — 6 x + 2 ‘ = 1 10 · 3 x 2 3 — 2 x 2 — 6 = 1 10 · x 2 — x — 6
Далее определяем, когда она будет обращаться в 0 :
y » = 0 ⇔ 1 10 · ( x 2 — x — 6 ) = 0 ⇔ x 2 — x — 6 = 0 D = ( — 1 ) 2 — 4 · 1 · ( — 6 ) = 25 x 1 = 1 — 25 2 = — 2 , x 2 = 1 + 25 2 = 3
Мы нашли абсциссы двух вероятных точек перегиба – 2 и 3 . Все, что нам осталось сделать – это проверить, в какой точке производная изменит свой знак. Изобразим числовую ось и нанесем на нее данные точки, после чего расставим знаки второй производной на получившихся промежутках.
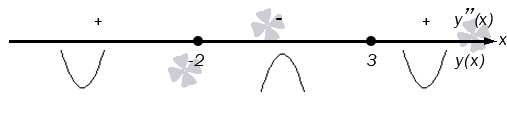
Дуги показывают направление выпуклости графика в каждом интервале.
Вторая производная меняет знак на противоположный (с плюса на минус) в точке с абсциссой 3 , проходя через нее слева направо, и также делает это (с минуса на плюс) в точке с абсциссой 3 . Значит, мы можем сделать вывод, что x = — 2 и x = 3 – это абсциссы точек перегиба графика функции. Им будут соответствовать точки графика — 2 ; — 4 3 и 3 ; — 15 8 .
Взглянем вновь на изображение числовой оси и получившиеся знаки на интервалах, чтобы сделать выводы о местах вогнутости и выпуклости. Получается, что выпуклость будет расположена на отрезке — 2 ; 3 , а вогнутость на отрезках ( — ∞ ; — 2 ] и [ 3 ; + ∞ ) .
Решение задачи наглядно изображено на графике: синий цвет – выпуклости, красный – вогнутость, черный цвет означает точки перегиба.
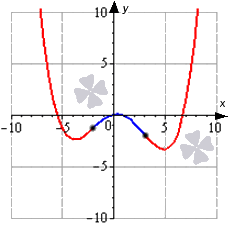
Ответ: выпуклость будет расположена на отрезке — 2 ; 3 , а вогнутость на отрезках ( — ∞ ; — 2 ] и [ 3 ; + ∞ ) .
Условие: вычислите абсциссы всех точек перегиба графика функции y = 1 8 · x 2 + 3 x + 2 · x — 3 3 5 .
Решение
Область определения заданной функции – множество всех действительных чисел. Вычисляем производную:
y ‘ = 1 8 · ( x 2 + 3 x + 2 ) · x — 3 3 5 ‘ = = 1 8 · x 2 + 3 x + 2 ‘ · ( x — 3 ) 3 5 + ( x 2 + 3 x + 2 ) · x — 3 3 5 ‘ = = 1 8 · 2 x + 3 · ( x — 3 ) 3 5 + ( x 2 + 3 x + 2 ) · 3 5 · x — 3 — 2 5 = 13 x 2 — 6 x — 39 40 · ( x — 3 ) 2 5
В отличие от функции, ее первая производная не будет определена при значении x , равном 3 , но:
lim x → 3 — 0 y ‘ ( x ) = 13 · ( 3 — 0 ) 2 — 6 · ( 3 — 0 ) — 39 40 · 3 — 0 — 3 2 5 = + ∞ lim x → 3 + 0 y ‘ ( x ) = 13 · ( 3 + 0 ) 2 — 6 · ( 3 + 0 ) — 39 40 · 3 + 0 — 3 2 5 = + ∞
Это значит, что через данную точку будет проходить вертикальная касательная к графику. Следовательно, 3 может быть абсциссой точки перегиба.
Вычисляем вторую производную. Также находим область ее определения и точки, в которых она обращается в 0 :
y » = 13 x 2 — 6 x — 39 40 · x — 3 2 5 ‘ = = 1 40 · 13 x 2 — 6 x — 39 ‘ · ( x — 3 ) 2 5 — 13 x 2 — 6 x — 39 · x — 3 2 5 ‘ ( x — 3 ) 4 5 = = 1 25 · 13 x 2 — 51 x + 21 ( x — 3 ) 7 5 , x ∈ ( — ∞ ; 3 ) ∪ ( 3 ; + ∞ ) y » ( x ) = 0 ⇔ 13 x 2 — 51 x + 21 = 0 D = ( — 51 ) 2 — 4 · 13 · 21 = 1509 x 1 = 51 + 1509 26 ≈ 3 , 4556 , x 2 = 51 — 1509 26 ≈ 0 , 4675
У нас получились еще две возможные точки перегиба. Нанесем их все на числовую прямую и разметим получившиеся интервалы знаками:
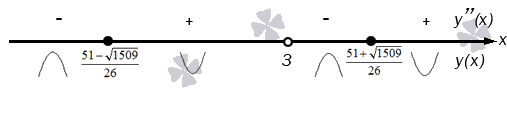
Перемена знака будет происходить при прохождении через каждую указанную точку, значит, они все являются точками перегиба.
Ответ: Изобразим график функции, отметив вогнутости красным, выпуклости синим и точки перегиба – черным:
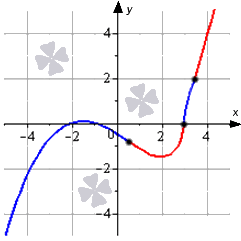
Зная первое достаточное условие перегиба, мы можем определить нужные точки, в которых не обязательно наличие второй производной. Исходя из этого, первое условие можно считать наиболее универсальным и пригодным для решения разных типов задач.
Отметим, что существует еще два условия перегиба, однако их можно применять только тогда, когда в указанной точке есть конечная производная.
Второе достаточное условие перегиба графика функции
Если мы имеем f » ( x 0 ) = 0 и f »’ ( x 0 ) ≠ 0 , то x 0 будет абсциссой точки перегиба графика y = f ( x ) .
Условие: задана функция y = 1 60 x 3 — 3 20 x 2 + 7 10 x — 2 5 . Определите, будет ли график функции иметь перегиб в точке 3 ; 4 5 .
Решение
Первое, что нужно сделать, – это убедиться в том, что данная точка вообще будет принадлежать графику этой функции.
y ( 3 ) = 1 60 · 3 3 — 3 20 · 3 2 — 2 5 = 27 60 — 27 20 + 21 10 — 2 5 = 9 — 27 + 42 — 8 20 = 4 5
Заданная функция определена для всех аргументов, являющихся действительными числами. Вычислим первую и вторую производные:
y ‘ = 1 60 x 3 — 3 20 x 2 + 7 10 x — 2 5 ‘ = 1 20 x 2 — 3 10 x + 7 10 y » = 1 20 x 2 — 3 10 x + 7 10 ‘ = 1 10 x — 3 10 = 1 10 ( x — 3 )
Мы получили, что вторая производная будет обращаться в 0 , если x будет равен 0 . Значит, необходимое условие перегиба для этой точки будет выполнено. Теперь используем второе условие: найдем третью производную и выясним, будет ли она обращаться в 0 при 3 :
y ‘ ‘ ‘ = 1 10 ( x — 3 ) ‘ = 1 10
Третья производная не будет обращаться в нуль ни при одном значении x. Поэтому можно заключить, что данная точка будет точкой перегиба графика функции.
Ответ: Покажем решение на иллюстрации:
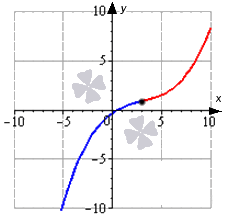
Третье достаточное условие перегиба графика функции
Допустим, что f ‘ ( x 0 ) = 0 , f » ( x 0 ) = 0 , . . . , f ( n ) ( x 0 ) = 0 и f ( n + 1 ) ( x 0 ) ≠ 0 .В таком случае при четном n мы получим, что x 0 – это абсцисса точки перегиба графика y = f ( x ) .
Условие: дана функция y = ( x — 3 ) 5 + 1 . Вычислите точки перегиба ее графика.
Решение
Данная функция является определенной на всем множестве действительных чисел. Вычисляем производную: y ‘ = ( ( x — 3 ) 5 + 1 ) ‘ = 5 · x — 3 4 . Поскольку она тоже будет определена для всех действительных значений аргумента, то в любой точке ее графике будет существовать невертикальная касательная.
Теперь вычислим, при каких значениях вторая производная будет обращаться в 0 :
y » = 5 · ( x — 3 ) 4 ‘ = 20 · x — 3 3 y » = 0 ⇔ x — 3 = 0 ⇔ x = 3
Мы получили, что при x = 3 график функции может иметь точку перегиба. Используем третье условие, чтобы подтвердить это:
y ‘ ‘ ‘ = 20 · ( x — 3 ) 3 ‘ = 60 · x — 3 2 , y ‘ ‘ ‘ ( 3 ) = 60 · 3 — 3 2 = 0 y ( 4 ) = 60 · ( x — 3 ) 2 ‘ = 120 · ( x — 3 ) , y ( 4 ) ( 3 ) = 120 · ( 3 — 3 ) = 0 y ( 5 ) = 120 · ( x — 3 ) ‘ = 120 , y ( 5 ) ( 3 ) = 120 ≠ 0
Имеем n = 4 по третьему достаточному условию. Это четное число, значит, x = 3 будет абсциссой точки перегиба и ей соответствует точка графика функции ( 3 ; 1 ) .
Ответ: Вот график данной функции с отмеченными выпуклостями, вогнутостями и точкой перегиба: